Решить логарифмическое уравнение.
Приложения:
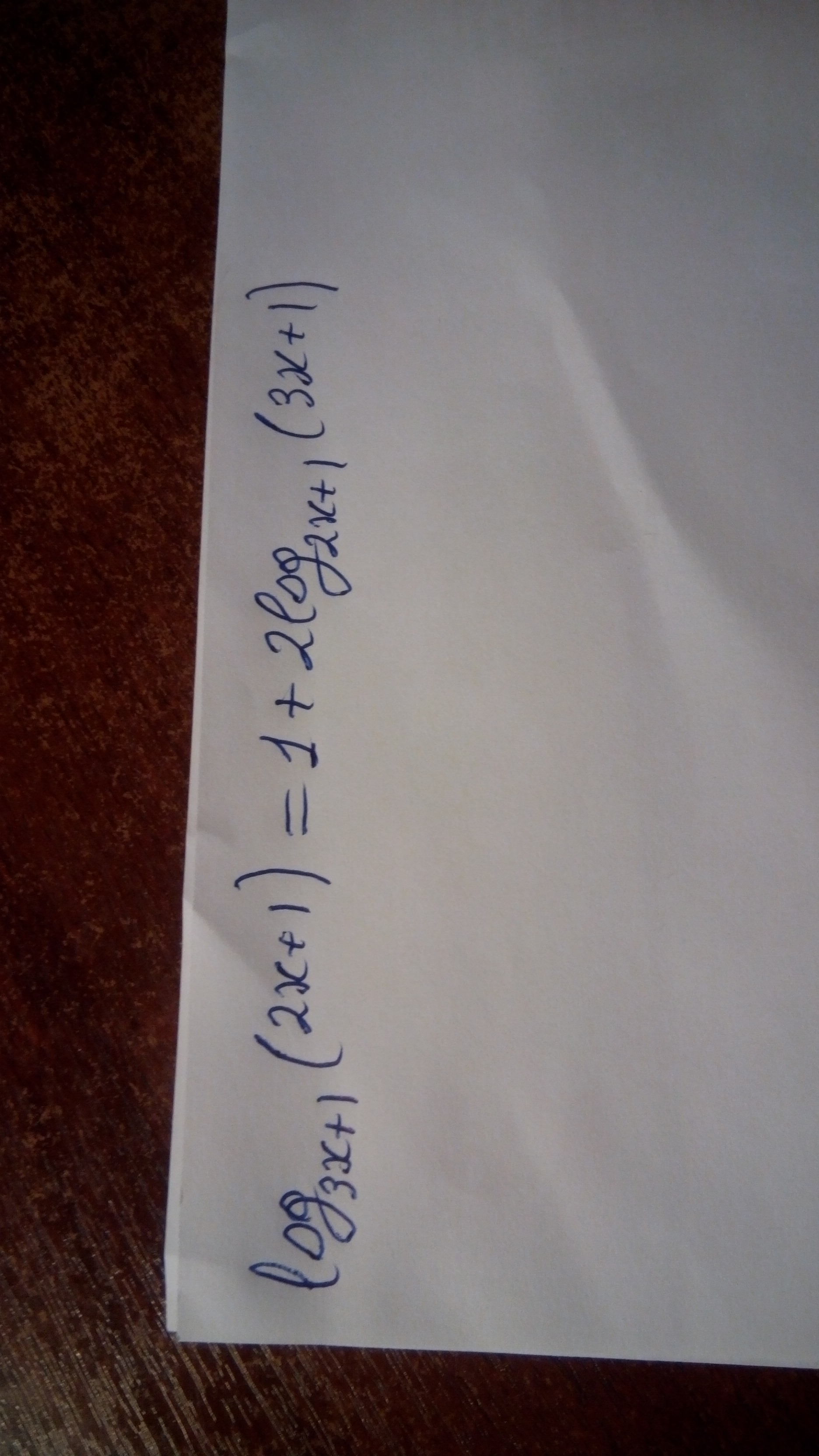
Ответы на вопрос
Ответил fadarm
0
ОДЗ: 3x+1>0 ⇒ x>-1/3; 2x+1>0 ⇒ x>-0,5; 3x+1≠1 ⇒ x≠0;
то есть ОДЗ является промежуток x∈(-1/3;0)∪(0;+∞)
Пусть
t²-t-2=0
D=9
t1=-1; t2=2
4x²+4x+1=1
4x(x+1)=0
x1=0; x2=-1 не подходит с учетом ОДЗ
2x+1=4x²+4x+1
2x(2x+1)=0
x3=0; x4=-0,5 не подходят с учетом ОДЗ
Данное уравнение не имеет корней
Новые вопросы