Решить логарифмическое уравнение:
Приложения:
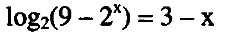
Ответы на вопрос
Ответил krugly1981
0
9 - 2^x = 2^3-x
9 - 2^x = 8 / 2^x
9*2^x - 2^2x = 8
пусть 2^x = y, тогда
9y - y² = 8
y² - 9y + 8 = 0
(y - 8)( y - 1)=0
y1 = 8
y2 = 1
2^x = 8 2^x = 1
x = 3 x = 0
Ответ: x1 = 3, x2 = 0.
9 - 2^x = 8 / 2^x
9*2^x - 2^2x = 8
пусть 2^x = y, тогда
9y - y² = 8
y² - 9y + 8 = 0
(y - 8)( y - 1)=0
y1 = 8
y2 = 1
2^x = 8 2^x = 1
x = 3 x = 0
Ответ: x1 = 3, x2 = 0.
Новые вопросы