Алгебра, вопрос задал Ифигения , 6 лет назад

Решить дифференциальное уравнение

Приложения:

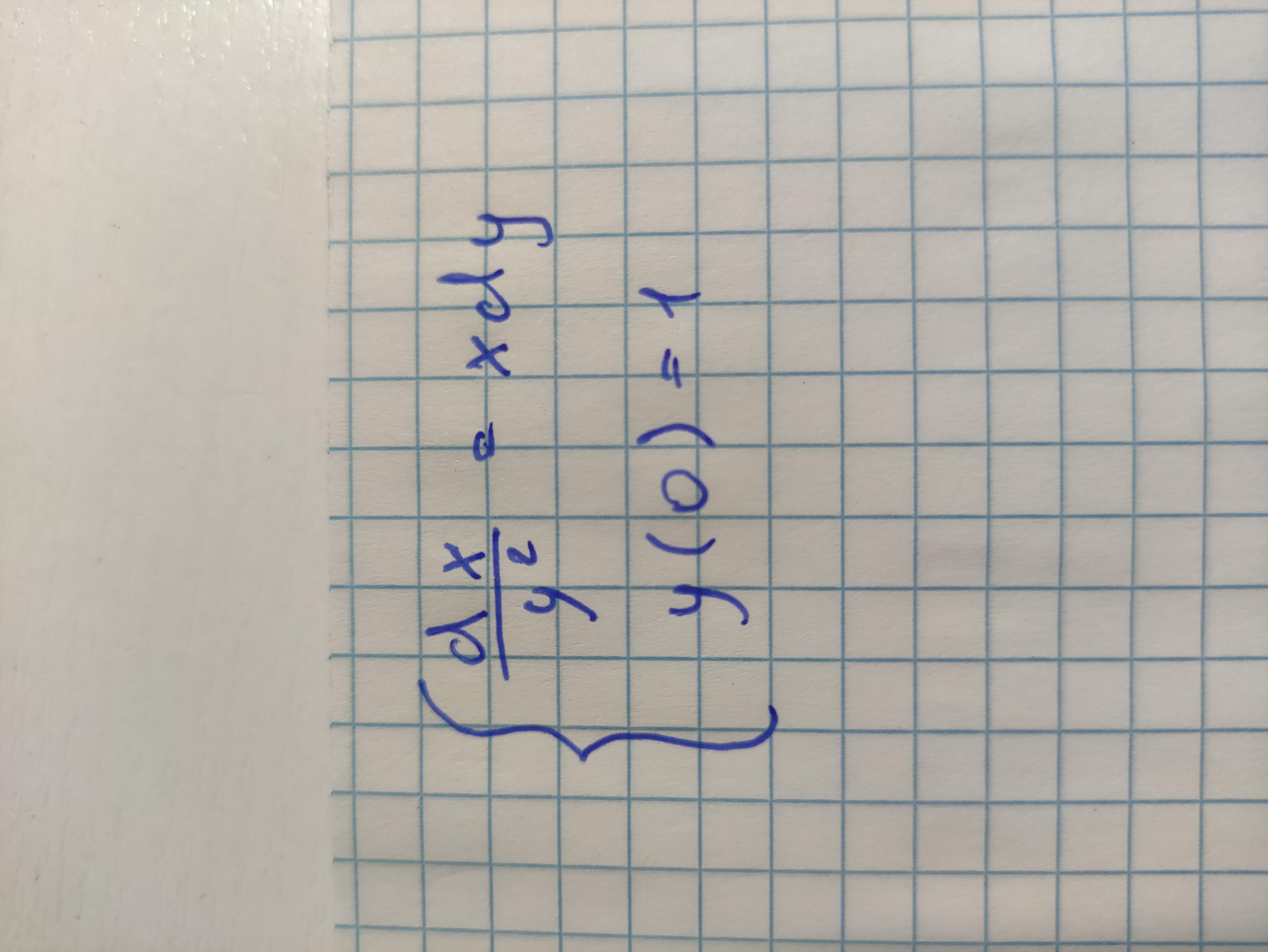
Ответы на вопрос

Ответил NNNLLL54

Ответ:

$\displaystyle \dfrac{dx}{y^2}=x\, dy\ \ \ ,\ \ \ y(0)=1\\\\\\\int \frac{dx}{x}=\int y^2\, dy\\\\\\ln|x|=\frac{y^3}{3}+\frac{C}{3}\ \ \ ,\ \ \ 3ln|x|=y^3+C\ \ ,\ \ \ \underline{\ y^3=3\, ln|x|-C\ }\ \ .\\\\\\y(0)=1:\ 1^3=3\, ln0-C$

Но ln0 не существует, поэтому задача Коши не имеет решения.

Если бы поменять значения "х" и "у" в начальных условиях, то

$y(1)=0:\ \ 0^3=3ln1-C\ \ ,\ \ 0=3\cdot 0-C\ \ ,\ \ C=0\ \ \Rightarrow \ \ y^3=3\, ln|x|$

Ответил Erann123

А если вот так записать, неправильно получится?

Приложения:

Предыдущий вопрос

Следующий вопрос

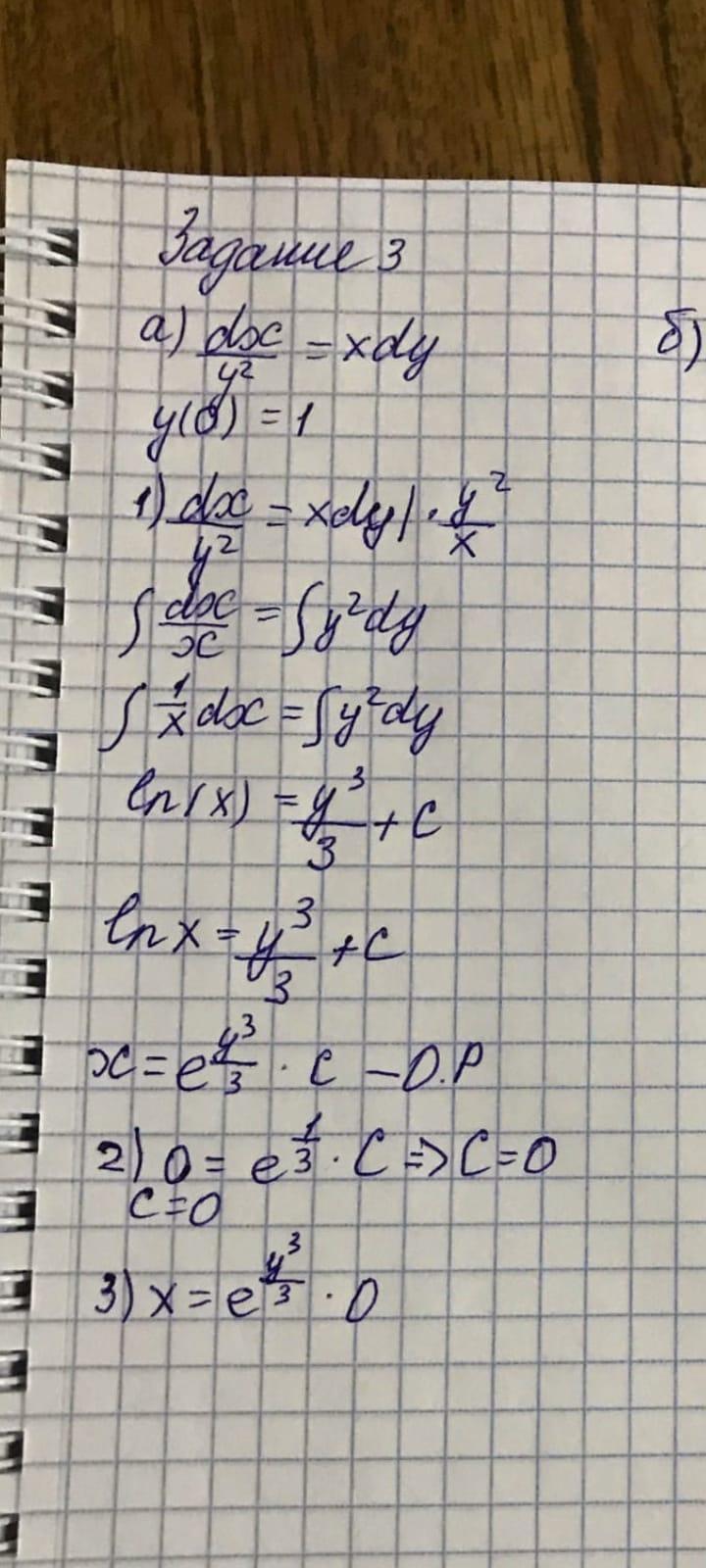
Новые вопросы

Русский язык, 1 год назад

СПАТЬ ПОРА! УСНУЛ БЫЧОК, ЛЁГ В КРОВАТКУ НА БОЧОК. СОННЫЙ МИШКА ЛЁГ В КРОВАТЬ, ТОЛЬКО СЛОН НЕ ХОЧЕТ СПАТЬ. ГОЛОВОЙ КИВАЕТ СЛОН, ОН СЛОНИХЕ ШЛЁТ ПОКЛОН. СЛОВА КАКИХ ЗНАКОМЫХ ТЕБЕ ЧАСТЕЙ РЕЧИ ЕСТЬ...

Русский язык, 1 год назад

Как разобрать слова по составу: Маленький,лёгенький,ельник,берёзонька,оленёнок, ёжонок,зайчата,пушистый, кораблик,овражек,учитель,сказочка,смелость, утята, библиотекарь, крючок,мячик и билетик.

Математика, 6 лет назад

Х:5=30:10, Х= вычесли и запиши ответ...

Математика, 6 лет назад

помогите пожалуйста ...

Математика, 8 лет назад

периметр 2-ух подобных треугольников 24 и 36 а площадь одного из них на 10больше площади другово .найдите площадь меньшего треугольника...

Литература, 8 лет назад

Напишите сочинение на тему "Жизненные ценности человека тогда и сейчас"пожалуйста Просьба не брать из интернета...