Решение системы линейных уравнений с двумя переменными способом сложения и способом подстановки. Урок 3
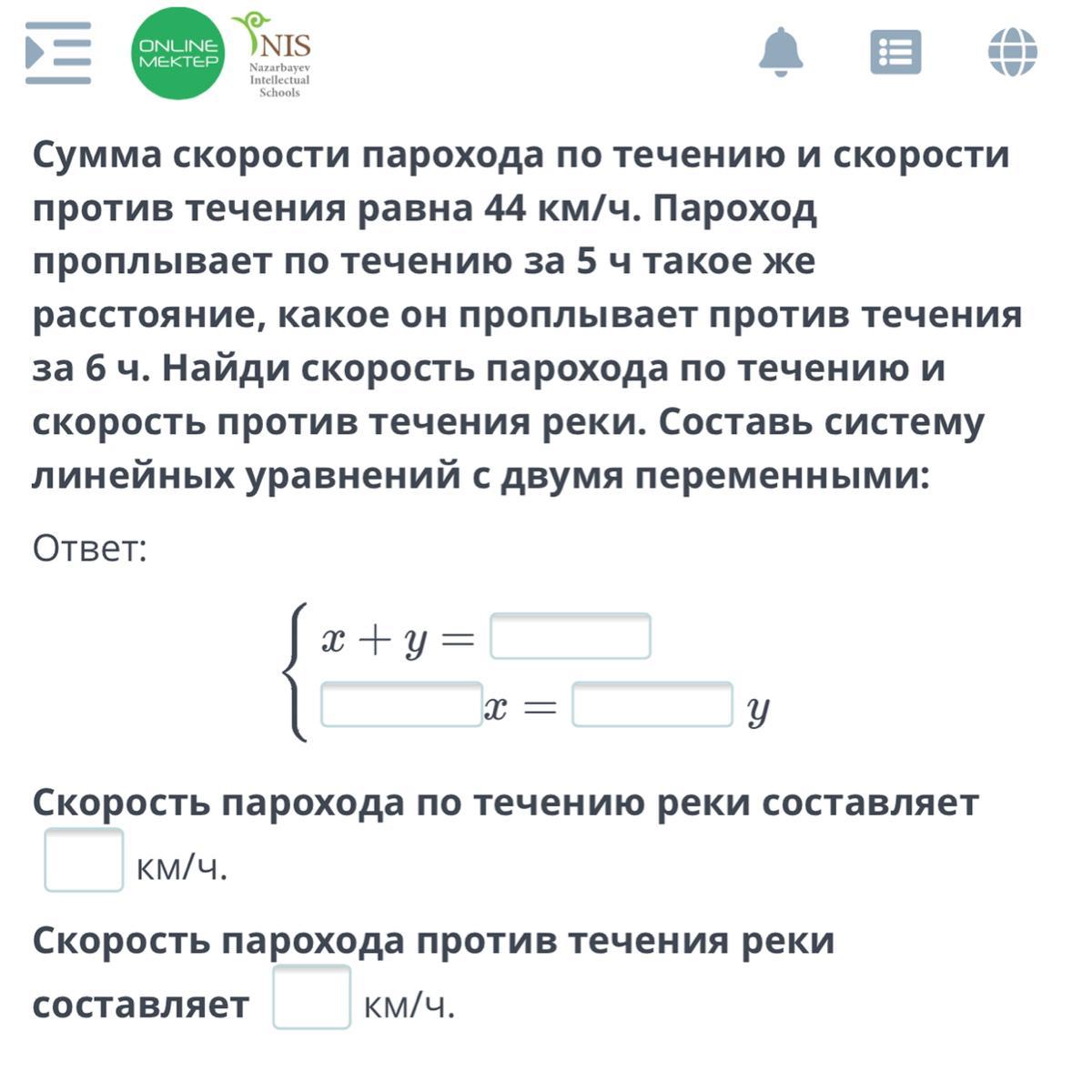
Сумма скорости парохода по течению и скорости против течения равна 44 км/ч. Пароход проплывает по течению за 5 ч такое же расстояние, какое он проплывает против течения за 6 ч. Найди скорость парохода по течению и скорость против течения реки. Составь систему линейных уравнений с двумя переменными:
Ответ:
Скорость парохода по течению реки составляет км/ч.
Скорость парохода против течения реки составляет км/ч.
Помогите
Приложения:
Ответы на вопрос
Ответил Iryn95
2
Пошаговое объяснение:
Сумма скорости парохода по течению и скорости против течения равна 44 км/ч.
Пусть скорость теплохода по течению - х км/час , а скорость теплохода против течения - у км/час , тогда получаем первое уравнение :
Пароход проплывает по течению за 5 ч такое же расстояние, какое он проплывает против течения за 6 ч.
Расстояние можно найти из формулы скорости :
Можем составить второе уравнение :
Получаем систему уравнений :
Выразим х через у в первом уравнении и подставим это значение во второе уравнение :
Мы нашли , что скорость теплохода против течения 20 км/час
Найдем скорость по течению :
км/час
ОТВЕТ : Скорость парохода по течению 24 км/час, скорость против течения 20 км/час
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Математика,
2 года назад
Математика,
8 лет назад