решение + рисунок к задаче ​

Ответ:

длина второй наклонной равна       см

Пошаговое объяснение:

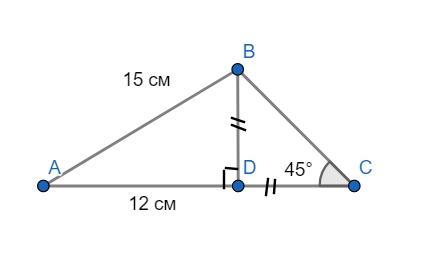
Из точки  В опустим перпендикуляр ВD  на прямую.

ΔABD  - прямоугольный. В нем нам известны гипотенуза и один катет.

Найдем другой катет (теорема Пифагора)

(см)

Теперь перейдем к треугольнику BDC.

ΔBDC  - равнобедренный, т.к наклонная ВС образует с прямой ∠45°.

Следовательно, DC = BD = 9см

Теперь найдем гипотенузу  BC  (это и будет вторая наклонная)

(см)