Ребятки(((((((((((подробное решение
Приложения:
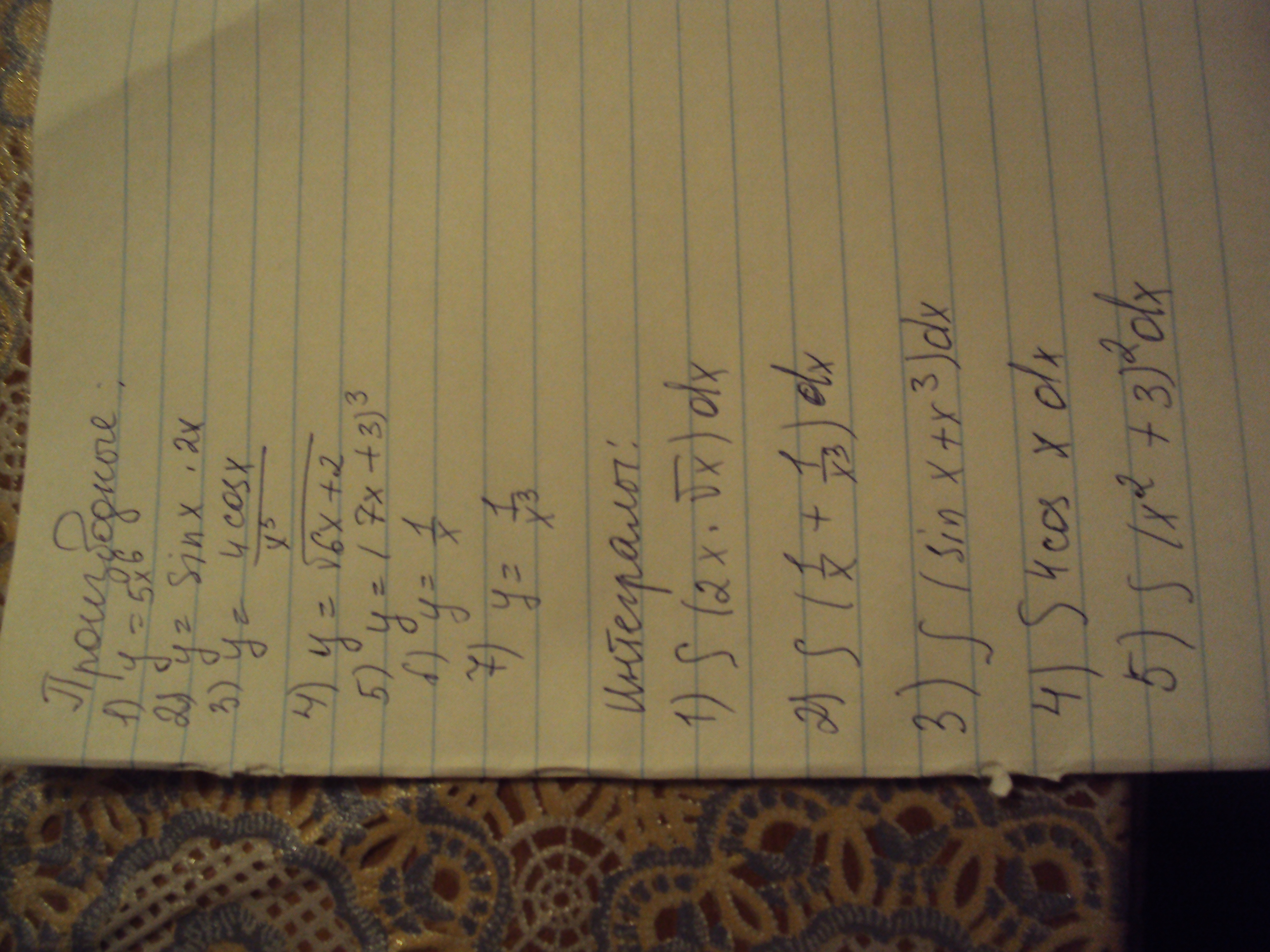
Ответы на вопрос
Ответил logophobia
0
Производные:
1) y' = (5x^6)' = 5*6x^(6–1) = 30x^5 ;
2) y' = (2xsinx)' = 2sinx + 2xcosx ;
3) y' = (4cosx/x^5)' = ( – 4 x^5 sinx – 5 x^(5–1) cosx ) / x^(2*5) =
= – ( 4 x sinx + 5 cosx ) / x^6 ;
4) y' = √[ 6x + 2 ] ' = ( ( 6x + 2 )^(1/2) )' = (1/2)( ( 6x + 2 )^(1/2–1) ) * 6 =
= 3 / ( 6x + 2 )^(1/2) = 3 / √[ 6x + 2 ] ;
5) y' = ( ( 7x + 3 )^3 )' = 3 ( ( 7x + 3 )^(3–1) ) * 7 = 21(7x+3)² ;
6) y' = (1/x)' = ( x^(–1) )' = (–1) ( x^(–1–1) ) = – x^(–2) = –1/x² ;
7) y' = (1/x³)' = ( x^(–3) )' = (–3) ( x^(–3–1) ) = –3x^(–4) = –3/x^4 ;
Интегралы:
1) ∫ 2x√x dx = ∫ 2x x^(1/2) dx = 2 ∫ x^(3/2) dx = 2/(3/2+1) x^(3/2+1) + C =
= 2/(5/2) x^(2+1/2) + C = (4/5) x²√x + C ;
2) ∫ (1/x+1/x³) dx = ∫ dx/x + ∫ x^–3 dx = ln|x| + x^(–3+1)/(–3+1) + C =
= ln|x| –(x^–2)/2 + C = ln|x| – 1/(2x²) + C ;
3) ∫ (sinx+x³) dx = ∫ sinx dx + ∫ x³dx = –cosx + (x^(3+1))/(3+1) + C =
= (x^4)/4 – cosx + C ;
4) ∫ 4cosx dx = 4 sinx + C ;
5) ∫ (x²+3)²dx = ∫ ( x^4 + 6x^2 + 9 ) dx = ∫ x^4 dx + 6 ∫ x²dx + 9 ∫ dx =
= (x^(4+1))/(4+1) + 6 (x^(2+1))/(2+1) + 9x + C = (x^5)/5 + 6 (x^3)/3 + 9x + C ;
1) y' = (5x^6)' = 5*6x^(6–1) = 30x^5 ;
2) y' = (2xsinx)' = 2sinx + 2xcosx ;
3) y' = (4cosx/x^5)' = ( – 4 x^5 sinx – 5 x^(5–1) cosx ) / x^(2*5) =
= – ( 4 x sinx + 5 cosx ) / x^6 ;
4) y' = √[ 6x + 2 ] ' = ( ( 6x + 2 )^(1/2) )' = (1/2)( ( 6x + 2 )^(1/2–1) ) * 6 =
= 3 / ( 6x + 2 )^(1/2) = 3 / √[ 6x + 2 ] ;
5) y' = ( ( 7x + 3 )^3 )' = 3 ( ( 7x + 3 )^(3–1) ) * 7 = 21(7x+3)² ;
6) y' = (1/x)' = ( x^(–1) )' = (–1) ( x^(–1–1) ) = – x^(–2) = –1/x² ;
7) y' = (1/x³)' = ( x^(–3) )' = (–3) ( x^(–3–1) ) = –3x^(–4) = –3/x^4 ;
Интегралы:
1) ∫ 2x√x dx = ∫ 2x x^(1/2) dx = 2 ∫ x^(3/2) dx = 2/(3/2+1) x^(3/2+1) + C =
= 2/(5/2) x^(2+1/2) + C = (4/5) x²√x + C ;
2) ∫ (1/x+1/x³) dx = ∫ dx/x + ∫ x^–3 dx = ln|x| + x^(–3+1)/(–3+1) + C =
= ln|x| –(x^–2)/2 + C = ln|x| – 1/(2x²) + C ;
3) ∫ (sinx+x³) dx = ∫ sinx dx + ∫ x³dx = –cosx + (x^(3+1))/(3+1) + C =
= (x^4)/4 – cosx + C ;
4) ∫ 4cosx dx = 4 sinx + C ;
5) ∫ (x²+3)²dx = ∫ ( x^4 + 6x^2 + 9 ) dx = ∫ x^4 dx + 6 ∫ x²dx + 9 ∫ dx =
= (x^(4+1))/(4+1) + 6 (x^(2+1))/(2+1) + 9x + C = (x^5)/5 + 6 (x^3)/3 + 9x + C ;
Ответил aykam98
0
спасибочки
Новые вопросы
Информатика,
2 года назад
Информатика,
2 года назад
Литература,
8 лет назад
Математика,
8 лет назад
Математика,
9 лет назад