Алгебра, вопрос задал dilnozalove2004 , 2 года назад

Ребятааа
Докажите тождество по братски
(у меня -1 получается)

Приложения:

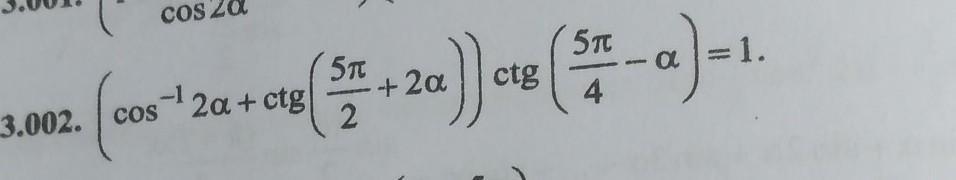
dilnozalove2004: ну блин пжлст

dilnozalove2004: если решишь получишь лучший ответ

Ответы на вопрос

Ответил kmike21

Ответ:

Объяснение:

Рассмотрим выражения по отдельности

$cos^{-1}2\alpha = \frac{1}{cos2\alpha }$

$ctg(\frac{5\pi }{2}+2\alpha) = ctg(2\pi +\frac{\pi }{2}+2\alpha)=ctg(\frac{\pi }{2}+2\alpha)=-tg2\alpha$

$ctg(\frac{5\pi }{4}-\alpha )= ctg(\pi +(\frac{\pi }{4}-\alpha) )=ctg(\frac{\pi }{4}-\alpha)$

также учтем, что

sin²α+cos²α=1

Получаем

$(cos^{-1}2\alpha +ctg(\frac{5\pi }{2}+2\alpha ))ctg(\frac{5\pi }{4} -\alpha )=(\frac{1}{cos2\alpha } -tg2\alpha )ctg(\frac{\pi }{4} -\alpha )=\\ = (\frac{1}{cos2\alpha } -\frac{sin2\alpha}{cos2\alpha} )ctg(\frac{\pi }{4} -\alpha )=$

$=\frac{1-sin2\alpha }{cos2\alpha } \frac{ctg\frac{\pi }{4} ctg\alpha +1}{ctg\alpha -ctg\frac{\pi }{4}} = \frac{sin^2\alpha +cos^2\alpha -2sin\alpha cos\alpha }{cos^2\alpha -sin^2\alpha } \frac{ ctg\alpha +1}{ctg\alpha -1} = \frac{(cos\alpha -sin\alpha)^2 }{(cos\alpha -sin\alpha) (cos\alpha +sin\alpha)} \frac{ ctg\alpha +1}{ctg\alpha -1}$

$= \frac{cos\alpha - sin\alpha }{cos\alpha + sin\alpha } \frac{ ctg\alpha +1}{ctg\alpha -1}=\frac{\frac{cos\alpha}{sin\alpha} - \frac{sin\alpha}{sin\alpha} }{\frac{cos\alpha}{sin\alpha} + \frac{sin\alpha}{sin\alpha} } \frac{ ctg\alpha +1}{ctg\alpha -1}=\frac{ctg\alpha - 1 }{ctg\alpha + 1 } \frac{ ctg\alpha +1}{ctg\alpha -1}=1$