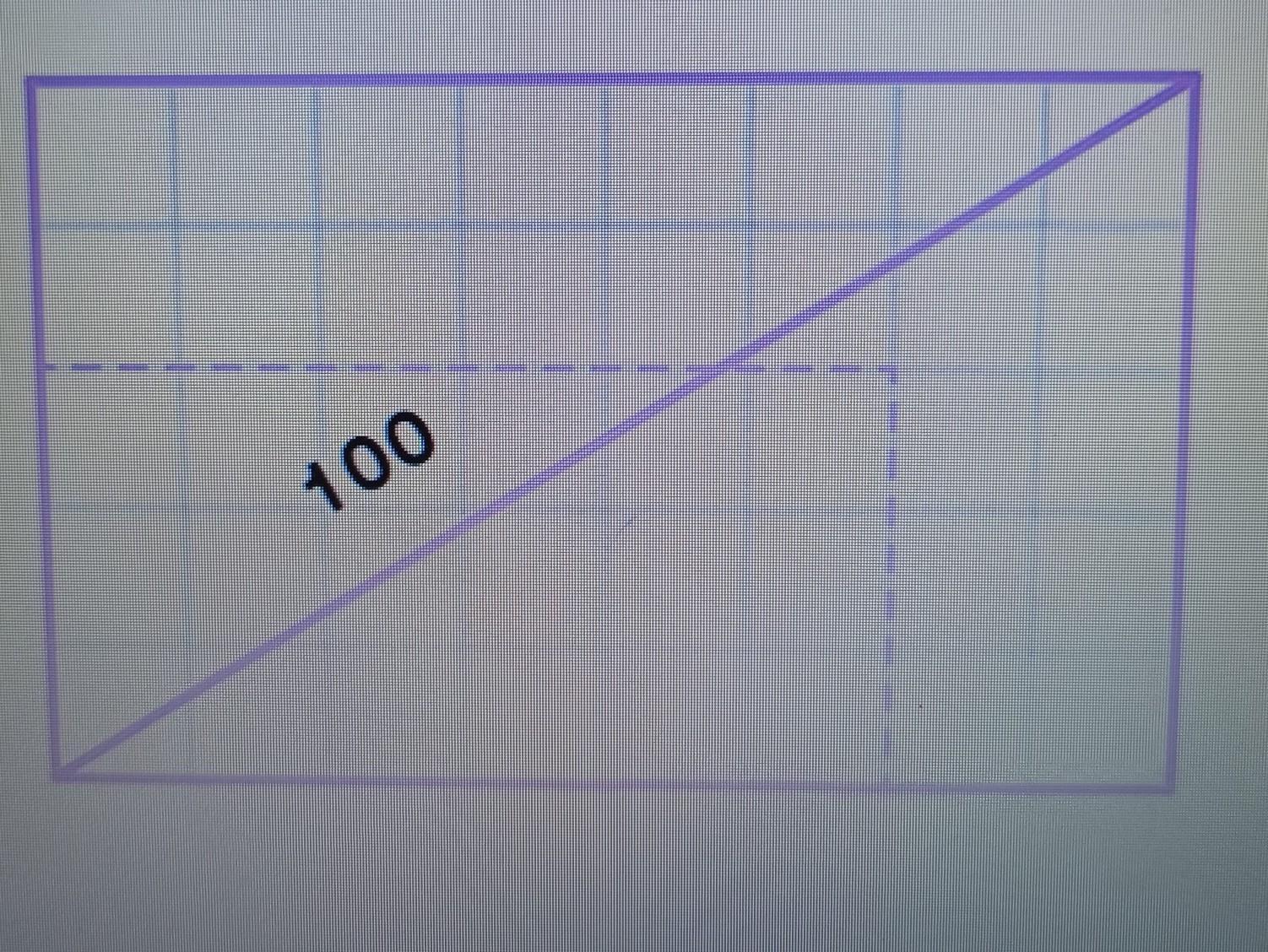
Ребята косипи траву на участке прямоугольной формы, диагональ которого 100 метров. На отдыхе, они заметили, что уменьшили длину некошенного поля на 40 метра, а ширину на 30 метров, сохранив его форму При этом периметр поля уменьшился в 2 раза. Определи диагональ нового поля
Приложения:
Ответы на вопрос
Ответил bel72777
2
Ответ:
50
Пошаговое объяснение:
a - начальная длина участка, м.
b - начальная ширина участка, м.
Используем формулы:
теорема Пифагора a²+b²=c²;
периметр прямоугольника P=2(a+b).
Система уравнений:
a²+b²=100²
2·2(a-40+b-30)=2(a+b) |2
2(a+b-70)=a+b
2a+2b-a-b=140
a=140-b
(140-b)²+b²=10000
19600-280b+b²+b²=10000
2b²-280b+19600-10000=0
2b²-280b+9600=0 |2
b²-140b+4800=0; D=19600-19200=400
b₁=(140-20)/2=120/2=60; a₁=140-60=80
b₂=(140+20)/2=160/2=80; a₂=140-80=60 - не подходит, так как длина всегда больше ширины.
Диагональ нового поля:
c²=(a-40)²+(b-30)²=(80-40)²+(60-30)²=1600+900=2500=50²
c=50 м
Новые вопросы