Алгебра, вопрос задал Maks71800 , 2 года назад

Ребят очень срочно пожалуйста
Вычислить границу функции.

Приложения:

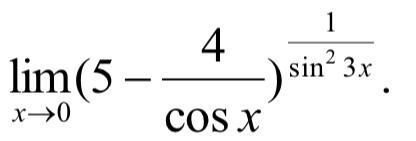
Ответы на вопрос

Ответил NNNLLL54
1

Ответ:

\lim\limits_{x \to 0}\, \Big(5-\dfrac{4}{cosx}\Big)^{\dfrac{1}{sin^23x}}=\lim\limits_{x \to 0}\Big(1+(4-\dfrac{4}{cosx})\Big)^{\dfrac{1}{sin^23x}}\ =

=\lim\limits_{x \to 0}\Big(1+\dfrac{4(cosx-1)}{cosx}\Big)^{\frac{cosx}{4(cosx-1)}}\Big)^{\frac{4(cosx-1)}{cosx}\cdot \frac{1}{sin^23x}}=\\\\\\=e^{\lim\limits_{x \to 0}\frac{-4\cdot 2sin^2\frac{x}{2}}{cosx\cdot sin^23x}}=e^{\lim\limits_{x \to 0}\frac{-8\cdot (x^2/4)}{cosx\cdot (3x)^2}}=e^{-\frac{2}{9}}

P.S.\ \ \ cosx-1=-(1-cosx)=-2sin^2\dfrac{x}{2}\\\\sina3x\sim 3x\ ,\ esli\ \ 3x\to 0\\\\sin\dfrac{x}{2}\sim \dfrac{x}{2}\ ,\ esli\ \dfrac{x}{2}\to 0\\\\cos0=1

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Қазақ тiлi, 1 год назад
Антоним и синоним слова Акылды...
Русский язык, 1 год назад
49.Прочитайте.Спишите , встовляя пропущенные буквы.
Физика, 2 года назад
Какую работу совершает газ, если внутренняя энергия уменьшилась на 100 Дж и при этом газ передал количество теплоты 0,6 кДж? 500 Дж 700 Дж -700 Дж -500 Дж СРОЧНОО помогите!!!​
Математика, 2 года назад
Незнайка прочитал 117 страниц, что составило 0,9 волшебной книги. Сколько страниц в волшебной книге? Помогите!!!
Физика, 7 лет назад
Тележка массой 1 кг движется со скоростью 8 м/с навстречу тележке массой 2 кг, движущейся со скоростью 3,5 м/с. После столкновения тележки соединяются и продолжают движение как единое целое. Какова...
Алгебра, 7 лет назад
найдите допустимое значене выражения 8/√х-5 (-5 не под корнем)...