Математика, вопрос задал ske46hbhj , 1 год назад

Ребят, нужно подробное решение со всеми пояснениями! Буду очень благодарен за РАЗВЁРНУТЫЙ ответ!

Приложения:

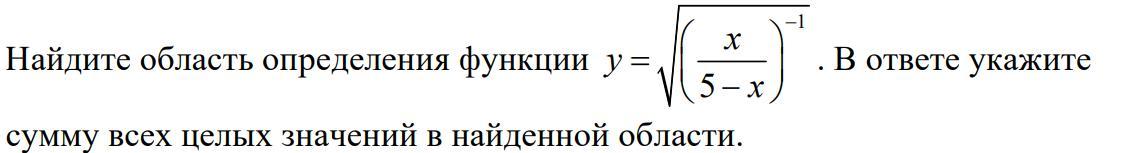
hderyb: Извиняюсь, но вам разве не решили уже?

ske46hbhj: там не понятно, что правильно

hderyb: Тоже на самом деле запутался))) но я бы, наверное, так же как там решал

ВикаБач: y=sqrt((5-x)/x)=sqrt(5/x -1); 5/x - 1 >= 0; 5/x >= 1l 0 < x <= 5; Далее не совсем понятео, "целых значений" ЧЕГО? Если аргумента, то 1+2+3+4+5=18, если функции, то бесконечность 0+1+2+3+4+5+6+......

ГАЗ52: у=√((х/(5-х))^(-1)),
область определения у=√((5-х)/х),
(5-х)/х≥ 0
х∈(0;5].
Целые 1+2+3+4+5=15

ГАЗ52: "...Далее не совсем понятео, "целых значений" ЧЕГО? Если..

ГАЗ52: В вопросе НАЙДЕННОЙ ОБЛАСТИ

ВикаБач: В вопросе "... сумму всех целых значений в найденной области...", но не уточнено значений ЧЕГО, значений аргумента или значений функции в этой области. Спасибо за арифметику, конечно 15, :)))

ГАЗ52: Найти область определения.......сумму целых значений в найденной области.

ВикаБач: :)) "сумму целых значений" ЧЕГО? Возможны варианты "...сумму целых значений ФУНКЦИИ в найденной области". и "...сумму целых значений АРГУМЕНТА ФУНКЦИИ в найденной области" :))