Алгебра, вопрос задал moetyan , 7 лет назад

Ребят мне очень срочно!!!!
Найти общее решение( или общий интеграл) дифференциального уравнения с разделяющимися переменными:

Приложения:

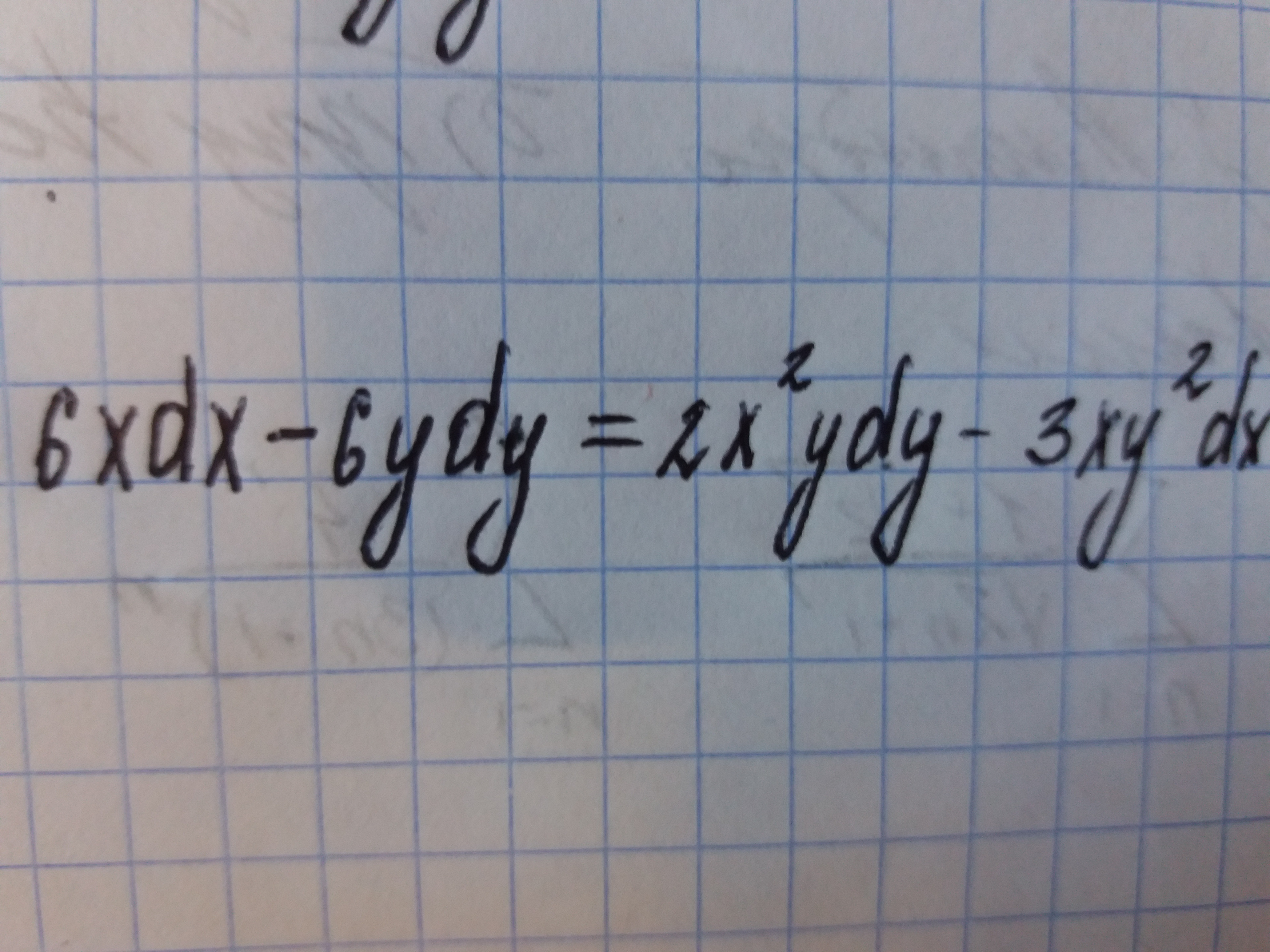
Ответы на вопрос

Ответил NNNLLL54

0

$6x, dx-6y, dy=2x^2y, dy-3xy^2, dx\\6x, dx+3xy^2, dx=2x^2y, dy+6y, dy\\3x(2+y^2), dx=2y(x^2+3), dy\\int frac{3x, dx}{x^2+3}=int frac{2y, dy}{2+y^2} \\frac{3}{2}int frac{2x, dx}{x^2+3}=int frac{d(y^2+2)}{y^2+2}quad Big [; int frac{du}{u}=ln|u|+C; Big ]\\frac{3}{2}int frac{d(x^2+3)}{x^2+3}=ln|y^2+2|\\frac{3}{2}cdot ln|x^2+3|=ln|y^2+2|+C\\\star ; ; d(x^2+3)=2x, dx; ; ,; ; d(y^2+2)=2y, dy; ; star$

Ответил moetyan

0

Вы мой спаситель, помогите с крайним: https://znanija.com/task/30249523

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

природу нужно беречь,потому что...

Русский язык, 1 год назад

место где растут березы...

Математика, 7 лет назад

ПОМОГИТЕ ПОЖАЛУЙСТА Выполни деление: (36xy):(4x). заранее СПАСИБО...

Математика, 7 лет назад

Решите пожалуйста задачу очень надо!!!! На дне рождения у Тани было съедено 9 заварных пирожных, 6 песочных и 3 бисквитных. Тех, кто съел 2 пирожных, в двое меньше тех, кто съел одно, а съевших 3...

Алгебра, 8 лет назад

помогите пожалуйста: 14b^3 c^2 -------------- = 16b^2 c...

Математика, 8 лет назад

при постройке здания требовалось вынуть 4500 м3 в определенный срок. перевыполняя дневную норму на 45м3, строители уже за 4 дня до срока выполнили 96% задания. определите сроки работы.