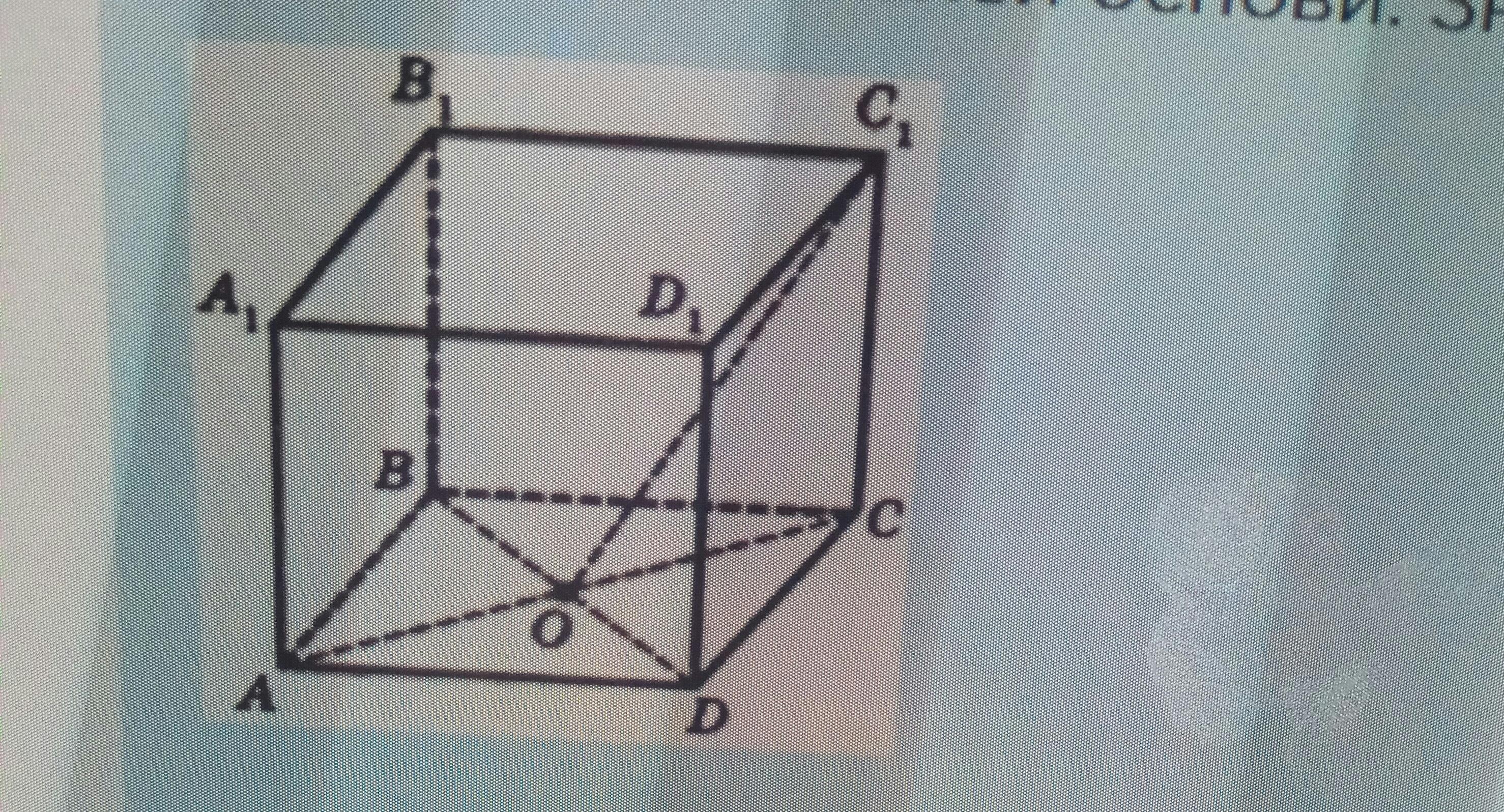
Ребро куба АВСDA1B1C1D1 равно а см ( рисунок на фото). B1D- диагональ куба, точка О - точка пересечения диагоналей основы. Найдите расстояние между BD и CC1.
Приложения:
Ответы на вопрос
Ответил DEE22
1
Ответ:
Пусть А - начало координат
Ось X -AB
Ось Y -AD
Ось Z -AA1
Расстояние между скрещивающимися прямыми равно модулю смешаного произведения
| АВ* ( ВВ1xAC) | деленому на модуль векторного произведения
| ВВ1хАС |
АВ(а;0;0)
ВВ1(0;0;а)
АС(а;а;0)
L= | AB * (BB1xAC) | / | BB1xAC |=
a^3/√(a^4+a^4)=√2a/2
Ответил Аноним
0
Ответ:
а√2/2
Объяснение:
АС=АВ√2=а√2 диагональ квадрата ABCD.
ОС=АС/2=а√2/2. Расстояние от BD до СС1
Новые вопросы
Русский язык,
2 года назад
Математика,
7 лет назад