Алгебра, вопрос задал Murex , 7 лет назад

Разложить на множители номера 6, 8, 10

Приложения:

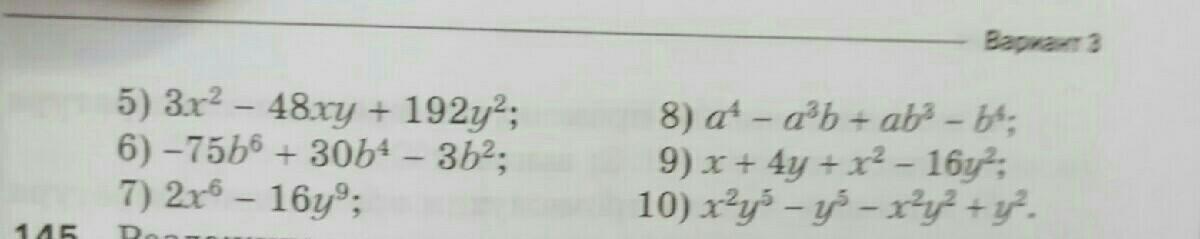
Ответы на вопрос

Ответил Tanda80

6)
$- 75 {b}^{6} + 30 {b}^{4} - 3 {b}^{2} = \ = - 3 {b}^{2} (25 {b}^{4} - 10 {b}^{2} + 1) = \ = - 3 {b}^{2} ( {(5 {b}^{2} )}^{2} - 2 times 5 {b}^{2} times 1 + 1) = \ = - 3 {b}^{2} {(5 {b}^{2} - 1)}^{2}=\= -3 {b}^{2} {(5 {b}^{2} - 1)}{(5 {b}^{2} - 1)}$
8)
${a}^{4} - {a}^{3} b + a {b}^{3} - {b}^{4} = \ = ( {a}^{4} - {a}^{3}b) + (a {b}^{3} - {b}^{4}) = \ = {a}^{3}(a - b) + {b}^{3}(a - b) = \ = (a - b)( {a}^{3} + {b}^{3} ) = \ = (a - b)(a + b)( {a}^{2} - ab + {b}^{2})$
10)
${x}^{2} {y}^{5} - {y}^{5} - {x}^{2} {y}^{2} + {y}^{2} = \ = ( {x}^{2} {y}^{5} - {y}^{5}) - ( {x}^{2} {y}^{2} - {y}^{2}) = \ = {y}^{5}( {x}^{2} - 1) - {y}^{2} ( {x}^{2} - 1) = \ = ( {x}^{2} - 1)( {y}^{5} - {y}^{2}) = \ = (x - 1)(x + 1) {y}^{2} ( {y}^{3} - 1) = \ = (x - 1)(x + 1) {y}^{2}(y - 1)( {y}^{2} + y + 1)$
Во всех задачах используем формулы сокращенного умножения.

Ответил Murex

Спасибо

Ответил Tanda80

Пожалуйста!

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

составить диалог из 2 человек,один из них болеет...

Русский язык, 1 год назад

морфологический разбор слова весенний ; морфемный разбор слова поровозный...

Биология, 7 лет назад