Математика, вопрос задал kotiklikol , 2 месяца назад

Разложить функцию в ряд Маклорена или Тейлора.

Приложения:

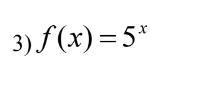
Ответы на вопрос

Ответил Alnadya

Решение .

Известно разложение в ряд Маклорена функции $\bf y=e^{\alpha }$ .

$\bf e^{\alpha }=1+\dfrac{\alpha }{1!}+\dfrac{\alpha ^2}{2!}+\dfrac{\alpha ^3}{3!}+...+\dfrac{\alpha ^{n}}{n!}+...\ \ \ ,\ \ \ \alpha \in R\ \ \ \ (*)$

По свойствам логарифма и показательной функции преобразуем выражение 5ˣ к виду

$\bf 5^{x}=e^{ln5^{x}}=e^{x\cdot ln5}$

В разложении (*) заменим α на х·ln5 :

$\displaystyle \bf 5^{x}=e^{x\cdot ln5}=1+\frac{x\cdot ln5}{1!}+\frac{x^2\cdot ln^25}{2!}+\frac{x^3\cdot ln^35}{3!}+\frac{x^{n}\cdot ln^{n}5}{n!}+...\ \ ,\ \ x\in R$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Геометрия, 2 месяца назад

Користуючись малюнком, укажи градусну міру кута 3, якщо ∠8 = 130º, а прямі a і b паралельні Виберіть одну відповідь: 130º 40º 50º 60º...

Алгебра, 2 месяца назад

допоможіть будьласка, фотографія нижче...

Экономика, 2 месяца назад

Завдання 3.6. Середньооблікова чисельність працівників підприємства за рік склала 7092 чол. Протягом року прийнято на роботу 400 чол., звільнено у зв'язку з навчанням і службою в армії 180 чол., за...

Математика, 2 месяца назад

обчислити наближено arctg0,97...

Химия, 6 лет назад

Основания. Лабораторный опыт № 8 «Изучение свойств оснований» Классифицируй основания по растворимости в воде. Гидроксид никеля (ІІ) . Гидроксид цинка . Гидроксид лития . Гидроксид калия .

Математика, 6 лет назад

5. Мама купила 5 тарелок и 3 пиалы по одинаковой цене. За тарелки она заплатила 10 000 сумов. Сколько стоят пиалы? Только с условий!!!