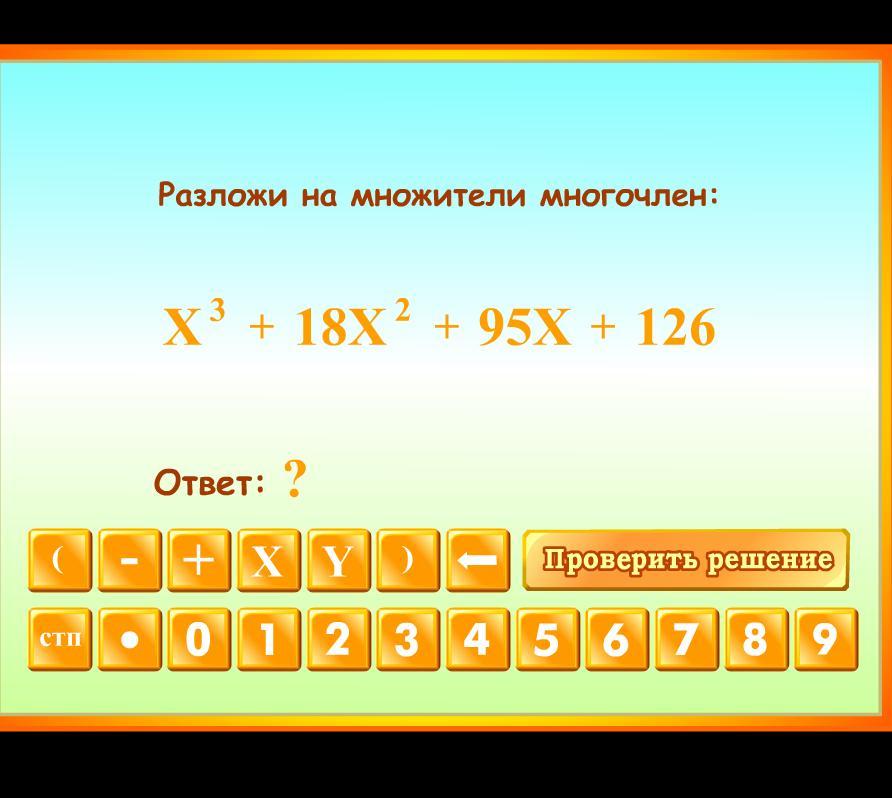
Алгебра, вопрос задал dmitrybborisov , 2 года назад

Разложи на множители многочлен

Приложения:

Ответы на вопрос

Ответил Alnadya

Решение.

Cначала подберём один из корней , являющихся делителем свободного члена, числа 126 . Им будет число -2 , так как

$(-2)^3+18(-2)^2-95\cdot 2+126=0$ . Значит многочлен делится нацело на (х+2) . Выделим этот множитель в многочлене .

$\bf x^3+18x^2+95x+126=(x^2+2x^2)+16x^2+95x+126=\\\\=x^2(x+2)+(16x^2+32x)+63x+126=\\\\=x^2(x+2)+16x(x+2)+(63x+126)=\\\\x^2(x+2)+16x(x+2)+63(x+2)=\\\\=(x+2)(x^2+16x+63)\\\\\\{}\ \ \ \star \ \ x^2+16x+63=0\ \ ,\ \ D=16^2-4\cdot 63=4\ \ ,\\\\x_1=\dfrac{-16-2}{2}=-9\ \ ,\ \ x_2=\dfrac{-16+2}{2}=-7\ \ ,\\\\x^2+16x+63=(x+9)(x+7)\ \star\\\\\\(x+2)(x^2+16x+63)=(x+2)(x+9)(x+7)$

Ответ: $\bf x^3+18x^2+95x+126=(x+2)(x+7)(x+9)$ .

dmitrybborisov: Почему -2 ведь это число делится и на 6

Alnadya: 126 делится на (-2) , затем проверяем, подставляя (-2) вместо х в уравнение, чтобы верное равенство получилось. При подстановке 6 в уравнение получим слева 1560, а нужен 0 , значит 6 не подойдёт, и не будет корнем . Ясно, что нужно отрицательное число подобрать из всех делителей . Если проверить, например, (-6), то слева -12 получим, но асё равно не 0 . Значит, дальше подбираем отрицательные делители .

Alnadya: в ответе проверка корня (-2) показана в 3 строчке

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Ребята помогите перевести пожалуйста )) I swim in the morning, my brother swims in the morning too. We feed our djgs in the afternoon, he feeds his dog in the morning. They cook in the evening,...

Русский язык, 1 год назад

Допиши окончания одушевлённых и неодушевлённых существительных в именительном и винительном падежах множественного числа. И.п. Кто? Инженеры, учитель, врачи, доктор. Что? Улицы, песен, облак,...

Алгебра, 2 года назад

В обменном пункте 5 серебряных монет обменивают на 3 золотых и 1 медную монеты. У мальчика Никиты были только серебряные монеты и когда он их обменял, то получил 50 медных монет. Вопрос-сколько...

Математика, 2 года назад

для приготовления ягодного компота необходима смесь из 6 частей вишни 4 частей клубники з частей смородины 2 частей малины сколько килограмм каждых ягод понадобится для 2,4такой смеси...

Математика, 7 лет назад

5x-3|y+2| при x=-2,y=-4...

Химия, 7 лет назад

Допоможіть, будьласка Треба зробити рівняння повне скорочене йоний вигляд 2CH3COOH+Zn(OH)2=(CH3COO)2Zn+2H2O...