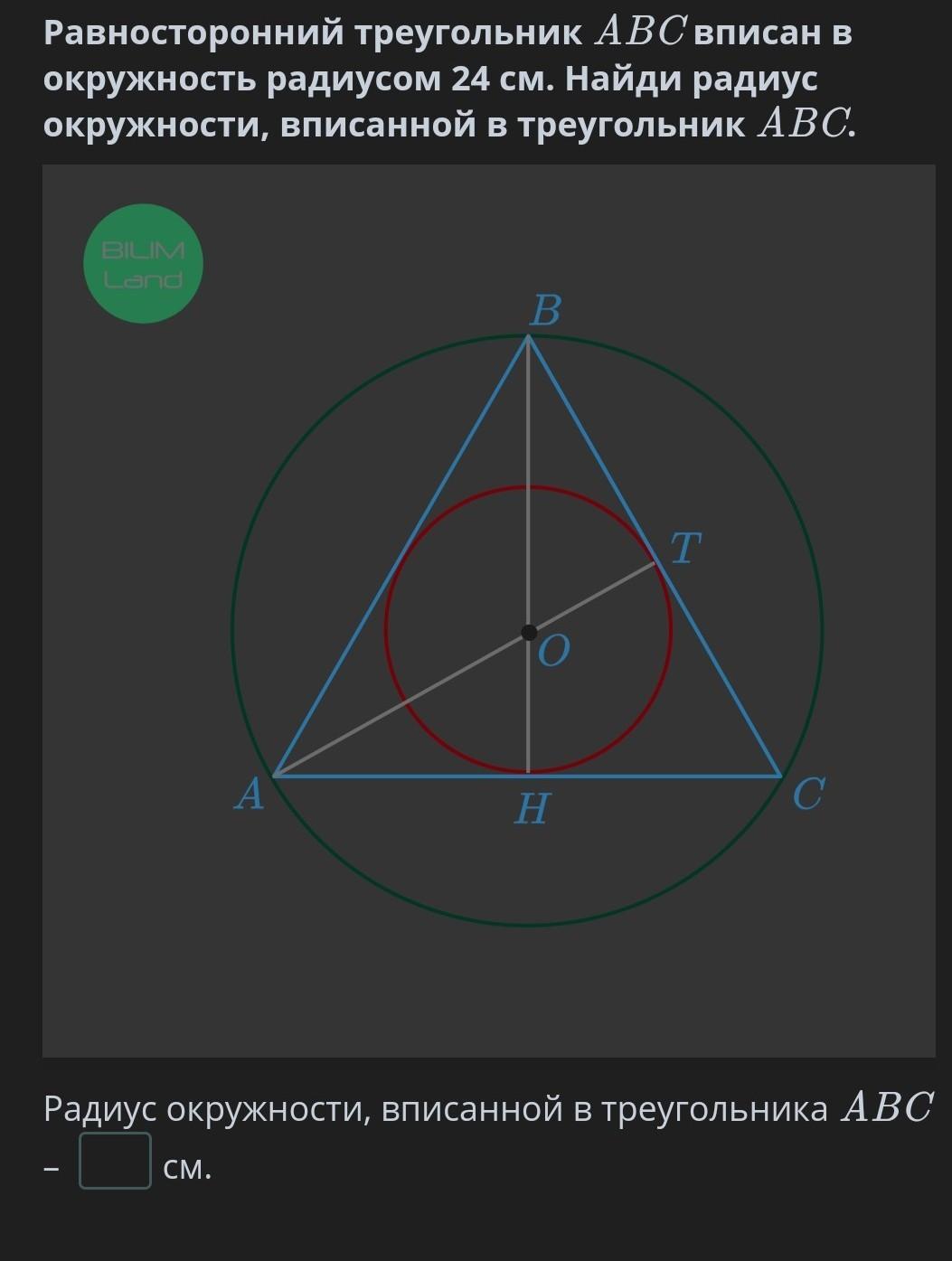
Равносторонний треугольник ABC вписан в окружность радиусом 24 см. Найди радиус окружности, вписанной в треугольник ABC.​

Ответ:

12 см

Объяснение:

В правильном треугольнике центры вписанной и описанной окружности совпадают.

Эта точка - точка пересечения медиан (биссектрис, высот).

Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины, значит радиус описанной окружности (ОВ) в два раза больше радиуса вписанной окружности (ОН):

ОВ = 24 см

ОН = 0,5 ОВ = 0,5 · 24 = 12 см