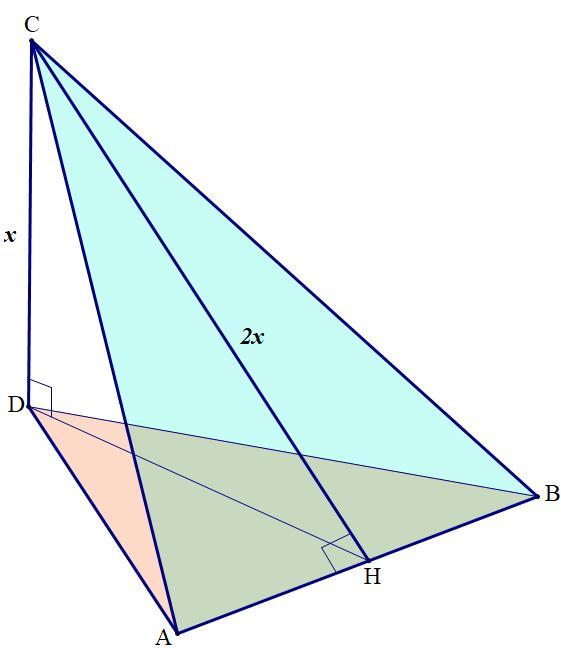
Расстояние от прямой АВ до точки (рис. 9) С в два раза больше расстояния от точки С до плоскости ABD, Найдите угол между плоскостями АВС и ABD
Ответы на вопрос
Ответ: 30°
Объяснение:
1. Расстояние от точки до прямой -- это перпендикуляр из этой точки к прямой.
CH ⊥ AB
Расстояние от точки до плоскости -- это перпендикуляр из этой точки к плоскости.
CD ⊥ (ABD)
2. CD ⊥ (ABD), DH c (ABD) ⇒ CD ⊥ DH (прямая, перпендикулярная плоскости, перпендикулярна любой прямой в этой плоскости)
3. CH -- наклонная, CD ⊥ (ABD) ⇒ DH -- проекция CH на плоскость (ABD).
4. CH -- накл., DH -- проекц., CH ⊥ AB ⇒ DH ⊥ AB (теорема о трёх перпендикулярах)
5. Угол между плоскостями -- это угол между перпендикулярами, проведёнными к их общему ребру.
(ABC) ∩ (ABD) = AB -- ребро
CH ⊥ AB, CH c (ABC); DH ⊥ AB, DH c (ABD) ⇒ ∠((ABC), (ABD)) = ∠DHC -- искомый
6. Пусть CD = x, тогда CH = 2x. Рассмотрим прямоугольный ΔCDH.
Катет в два раза меньше гипотенузы ⇒ ∠CHD = 30° (теорема об угле 30° в п/у Δ)