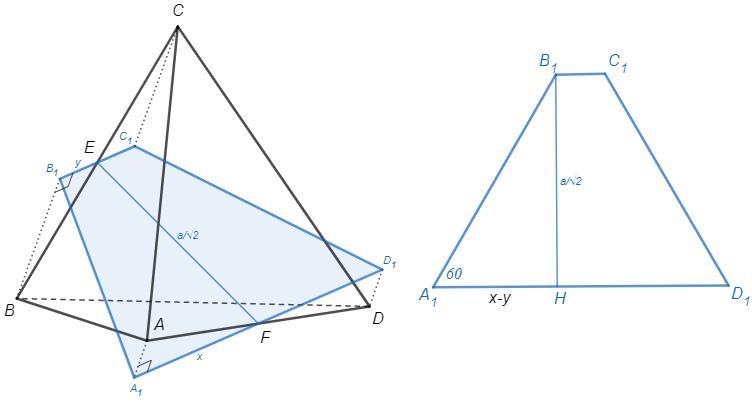
Рассмотрим плоскость, проходящую через середины двух противоположных ребер правильного тетраэдра. Проекция тетраэдра на эту плоскость - это четырехугольник с площадью А и одним из углов 60°. Найдите площадь поверхности тетраэдра.
Ответы на вопрос
E и F - середины ребер BC и AD.
EF - общий перпендикуляр к этим ребрам.
(Медианы BF и CF равны, BFC-р/б, EF⊥BC, медиана и высота. Аналогично EF⊥AD)
Точки B и C симметричны относительно EF, следовательно их проекции B1 и C1 тоже симметричны относительно EF. Аналогично A1 и D1. A1B1C1D1 - р/б трапеция.
Ребра BC и AD перпендикулярны.
(BF⊥AD, CF⊥AD => AD⊥(BFC) => AD⊥BC)
B1C1||A1D1 => ∠BEB1+∠AFA1=90° => ∠BEB1=∠FAA1
△BEB1=△FAA1 по гипотенузе и острому углу.
Рассмотрим трапецию
Пусть A1F=x, B1E=AA1=y, ребро=a
x^2 +y^2 =AF^2 =a^2/4 (△FAA1, т Пифагора) // 1
EF =√(BF^2-BE^2) =√(3/4 a^2 - a^2/4) =a/√2 =B1H
A1H =(A1D1-B1C1)/2 =x-y
B1H/A1H =tg60 => a/√2(x-y) =V3 // 2
A=mh =(x+y) a/√2 // 3
Три уравнения, три неизвестных. Найдем a.
x^2+y^2 =a^2/4
x-y =a/√6
x+y =A√2/a
x^2+y^2 - (x-y)^2 =2xy =a^2/4 -a^2/6 =a^2/12
x^2+y^2 + 2xy =(x+y)^2 =a^2/4 +a^2/12 =a^2/3
(x+y)^2 =2A^2/a^2 =a^2/3 => a^2=A√6
Полная поверхность правильного тетраэдра Sполн =a^2 √3
Sполн =A√6*√3 =3√2 A