Радиус основания конуса равен 20см,расстояние от центра основания до образующей равно 12 см . найдите площадь боковой поверхности конуса
Ответы на вопрос
Ответил Эль96
0
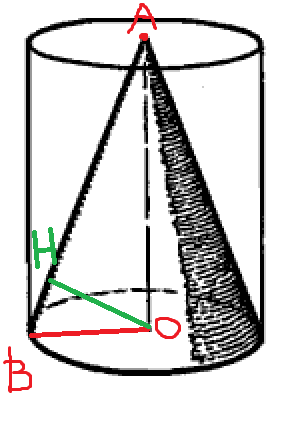
Конус.
т. О - центр основания конуса.
ОН - это расстояние от центра основания до образующей равно; - высота тр.АОВ.
OH=12
R=20
Sб.п.=Pi*R*L
1) Рассмотрим треугольник АОВ, в нём ОН - высота, значит, тр.АОВ и тр.НОВ - подобны(по двум углам: угол В - общий, и углы АОВ и ОНВ - по 90 градусов).
2) Найдём ВН:
По теореме Пифагора ВН²=20²-12²=400-144=256, значит ВН=16
3) Соотношение в подобных треугольниках:
ВА/ВО=АО/НО=ОВ/ВН
L=АВ-?
АВ/ВО=ВО/ВН
АВ=ВО²/НВ
АВ=400/16=25, т.е. L=25
4) Sб.п.=Pi*R*L=Pi*20*25=500Pi.
Ответ: 500Pi.
т. О - центр основания конуса.
ОН - это расстояние от центра основания до образующей равно; - высота тр.АОВ.
OH=12
R=20
Sб.п.=Pi*R*L
1) Рассмотрим треугольник АОВ, в нём ОН - высота, значит, тр.АОВ и тр.НОВ - подобны(по двум углам: угол В - общий, и углы АОВ и ОНВ - по 90 градусов).
2) Найдём ВН:
По теореме Пифагора ВН²=20²-12²=400-144=256, значит ВН=16
3) Соотношение в подобных треугольниках:
ВА/ВО=АО/НО=ОВ/ВН
L=АВ-?
АВ/ВО=ВО/ВН
АВ=ВО²/НВ
АВ=400/16=25, т.е. L=25
4) Sб.п.=Pi*R*L=Pi*20*25=500Pi.
Ответ: 500Pi.
Приложения:
Новые вопросы