Радиус окружности, вписанной в правильный шестиугольник, равен 2 см. Вычисли сторону шестиугольника HC и его площадь.
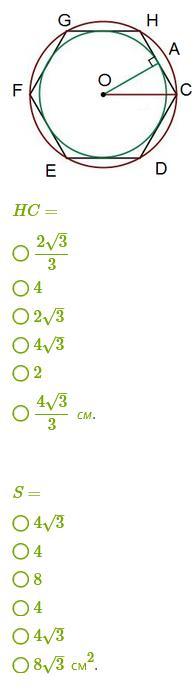
Ответы на вопрос
Ответ:
Ответ:
HC=\dfrac{4\sqrt{3}}{3}HC=
3
4
3
см
S = 8√3 см²
Объяснение:
а - сторона правильного шестиугольника,
r = 2 см - радиус вписанной окружности.
Найти: а, S.
Диагонали разбивают шестиугольник на 6 равных правильных треугольников.
ОК = r = 2 см - высота равностороннего треугольника СОН.
r=\dfrac{a\sqrt{3}}{2}r=
2
a
3
a=\dfrac{2r}{\sqrt{3}}=\dfrac{2\cdot 2}{\sqrt{3}}=\dfrac{4\sqrt{3}}{3}a=
3
2r
=
3
2⋅2
=
3
4
3
см
Площадь одного правильного треугольника:
S_1=\dfrac{a^2\sqrt{3}}{4}S
1
=
4
a
2
3
S_1=\dfrac{\left(\dfrac{4\sqrt{3}}{3}\right)^2\cdot \sqrt{3}}{4}=\dfrac{16\cdot 3\cdot \sqrt{3}}{9\cdot 4}=\dfrac{4\sqrt{3}}{3}S
1
=
4
(
3
4
3
)
2
⋅
3
=
9⋅4
16⋅3⋅
3
=
3
4
3
см²
Тогда площадь шестиугольника:
S=6S_1=6\cdot \dfrac{4\sqrt{3}}{3}=2\cdot 4\sqrt{3}=8\sqrt{3}S=6S
1
=6⋅
3
4
3
=2⋅4
3
=8
3
см²