Радиус окружности равен 10см .Найдите стороны вписанного в окружность правильного треугольника ,правильного четырехугольника , правильного шестиугольника .Пожалуйста с решениеи .

Начнем с самого простого:
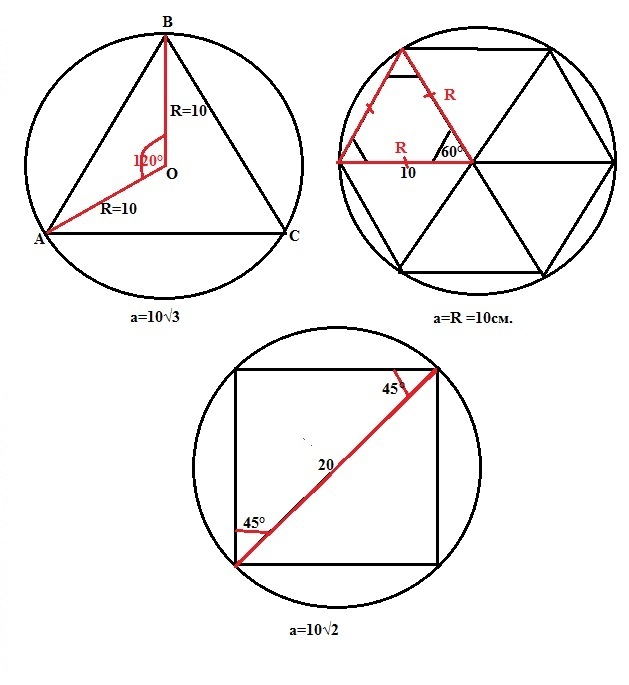
Сторона правильного шестиугольника равна радиусу описанной около него окружности (свойство). Но можно и так: диагонали правильного шестиугольника разбивают описанную окружность на 6 равных равносторонних треугольника (см. рисунок). Поэтому сторона этого шестиугольника равна радиусу описанной окружности.
Rш=10см.
Диагональ правильного четырехугольника (квадрата) равна диаметру описанной около него окружности (свойство). D=20см.
Тогда его сторона равна Rк= 10√2см.
Сторона правильного треугольника равна  R*√3 (формула). Или в нашем случае 10√3.
Но можно и без формулы: по теореме косинусов.
a² = 2*R²-2R²*Cos120° или a²=200*(1+1/2) = 100*3. a=√300 = 10√3см.
Ответ: сторона треугольника равна 10√3см, четырехугольника10√2см и шестиугольника 10см.