Рівняння, log3(x + 3) - log3(x - 1) = 1 - log3(4 - x)
Повна відповідь
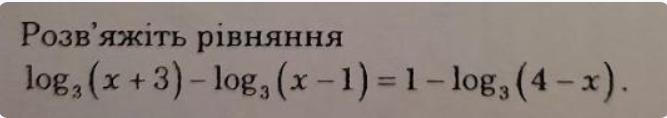
Ответы на вопрос
Ответ:Давайте розв'яжемо рівняння log3(x + 3) - log3(x - 1) = 1 - log3(4 - x) крок за кроком:
Використовуємо властивості логарифмів для спрощення рівняння. Зокрема, використаємо правило віднімання логарифмів:
log3[(x + 3)/(x - 1)] = 1 - log3(4 - x)
Використовуємо правило різниці логарифмів:
log3[(x + 3)/(x - 1)] = log3(3) - log3(4 - x)
Використовуємо правило логарифму бази 3:
(x + 3)/(x - 1) = 3 / (4 - x)
Множимо обидві частини рівняння на (x - 1) і (4 - x), щоб позбутися від знаменників:
(x + 3)(4 - x) = 3(x - 1)
Розкриваємо дужки та спрощуємо:
4x - x^2 + 12 - 3x = 3x - 3
Переносимо всі терміни на одну сторону рівняння:
-x^2 + 4x + 12 - 3x - 3x + 3 = 0
-x^2 - 2x + 15 = 0
Переносимо всі члени на протилежну сторону рівняння:
x^2 + 2x - 15 = 0
Факторизуємо квадратний тричлен:
(x + 5)(x - 3) = 0
Встановлюємо кожний множник рівний нулю і розв'язуємо два рівняння:
x + 5 = 0 або x - 3 = 0
x = -5 або x = 3
Отже, рівняння має два розв'язки: x = -5 та x = 3.
Объяснение: