пж пж пж помогите:(



Задача №1

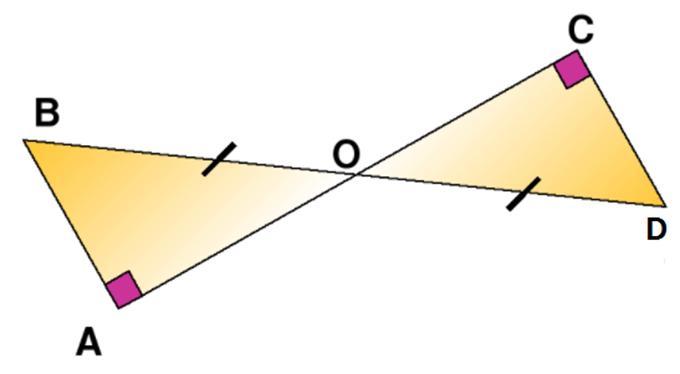
Дано два треугольника, ABO и CDO, BO=OD. Доказать что треугольник ABO= треугольник CDO, и по какому признаку!



Задача №2

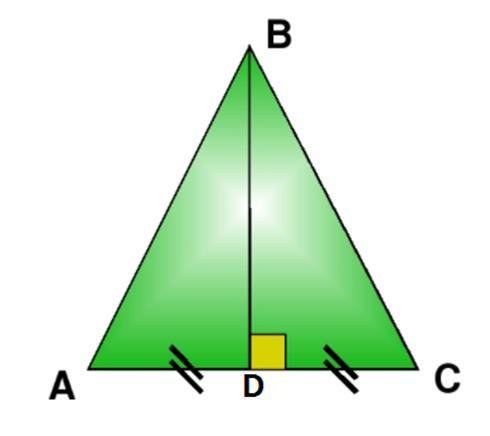
Дано два треугольника, ABD и CBD, AD=CD. Доказать что треугольник ABD= треугольник CBD, и по какому признаку!

Объяснение:

Задача №1

Дано два треугольника, ABO и CDO, BO=OD. Доказать что △ABO= △CDO.

△ABO и △CDO - прямоугольные ( ∠BAO=∠DCO=90°).

∠BOA=∠DOC, как вертикальные.

△ABO= △CDO по гипотенузе и острому углу.

• Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие теугольники равны.

Задача №2

Дано два треугольника, ABD и CBD, AD=CD. Доказать что △ABD=△CBD.

△ABD и △CBD - прямоугольные ( ∠BDA=∠BDC=90°).

BD - общая, следовательно △ABD=△CBD по двум катетам.

• Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (по первому признаку равенства треугольников).