Алгебра, вопрос задал Аноним , 1 год назад

пж помогите с алгеброй

Приложения:

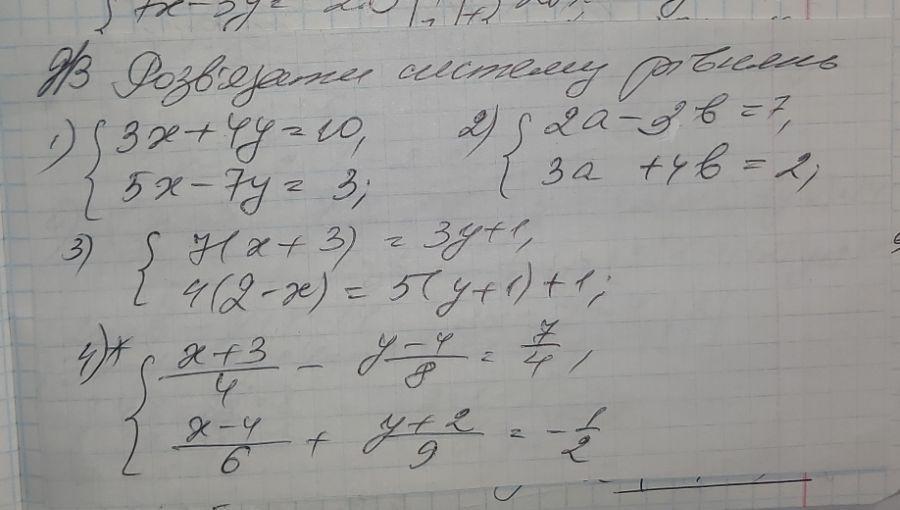
Ответы на вопрос

Ответил natalyabryukhova

Ответ:

1) (2; 1); 2) (2; -1); 3) (-2; 2); 4) (1; -2)

Объяснение:

Решить системы уравнений.

$\displaystyle \bf 1)\;\left \{ {{3x+4y=10} \atop {5x-7y=3}} \right.$

Решим методом сложения.

$\displaystyle \left \{ {{3x+4y=10\;\;\;|\cdot7} \atop {5x-7y=3\;\;\;|\cdot 4}} \right.\\$

$\displaystyle +\begin{cases}21x+28y=70\\\underline{20x-28y=12 } \end{cases} \\\\\;~\hspace{20px}41x +0=82\\\\x = \frac{82}{41}\\\\x=2$

Подставим значение х в первое уравнение и найдем у:

3 · 2 +4у = 10

4у = 10 - 6 |:4

y = 1

Ответ: (2; 1)

$\displaystyle \bf 2)\;\left \{ {{2a-3b=7} \atop {3a+4b=2}} \right.$

$\displaystyle \left \{ {{2a-3b=7\;\;\;|\cdot4} \atop {3a+4b=2\;\;\;|\cdot3}} \right.$

$\displaystyle +\begin{cases}8a-12b=28\\\underline{9a+12b=6 } \end{cases} \\\\\;~\hspace{20px}17a+0 = 34\\\\a = \frac{34}{17}\\\\a=2$

2 · 2 - 3b = 7

-3b = 7 - 4 |:(-3)

b = -1

Ответ: (2; -1)

$\displaystyle \bf 3)\; \left \{ {{7(x+3)=3y+1} \atop {4(2-x)=5(y+1)+1}} \right.$

Раскроем скобки:

$\displaystyle \left \{ {{7x+21=3y+1} \atop {8-4x=5y+5+1}} \right.$

Перенесем неизвестные влево, известные вправо, не забывая поменять знак на противоположный:

$\displaystyle \left \{ {{7x-3y=1-21} \atop {-4x-5y=6-8}} \right. \;\;\;\iff\;\;\; \left \{ {{7x-3y=-20\;\;\;|\cdot4} \atop {-4x-5y=-2\;\;\;|\cdot7}} \right. \\\\\\\displaystyle +\begin{cases}28x-12y=-80\\\underline{-28x-35y=-14 } \end{cases} \\\\\;~\hspace{20px}0 -47y= -94\\\\y = \frac{-94}{-47}\\\\y=2$

7 x - 3 · 2 = -20

7x = -20 + 6 |:7

x = -2

Ответ: (-2; 2)

$\displaystyle \bf 4)\;\left \{ {{\displaystyle\frac{x+3}{4} -\frac{y-4}{8} =\frac{7}{4} \atop {\displaystyle\frac{x-4}{6}+\frac{y+2}{9} =-\frac{1}{2} }} \right.$

Избавимся от знаменателей. Для этого умножим обе части первого уравнения на наименьшее общее кратное знаменателей. НОК(4;8) = 8.

Обе части второго уравнения умножим на НОК(6;9;2) = 18.

$\displaystyle 4)\;\left \{ {{\displaystyle\frac{x+3}{4} -\frac{y-4}{8} =\frac{7}{4} \;\;\;|\cdot8\atop {\displaystyle\frac{x-4}{6}+\frac{y+2}{9} =-\frac{1}{2} \;\;\;|\cdot18 }} \right.\\\\\\\left \{ {{2(x+3)-y+4=14} \atop {3(x-4)+2(y+2)=-9}} \right. \;\;\;\iff\;\;\;\left \{ {{2x+6-y+4=14} \atop {3x-12+2y+4=-9}} \right. \\\\\\\left \{ {{2x-y=14-10} \atop {3x+2y=-9+8}} \right. \;\;\;\iff\;\;\;\left \{ {{2x-y=4\;\;\;|\cdot2} \atop {3x+2y=-1}} \right.$