Алгебра, вопрос задал zhidckovanadej , 1 год назад

Прямоугольный треугольник с катетами 20 и 15 вращается вокруг гипотенузы.Найдите объем полученного тела вращения.Срочно!

Ответы на вопрос

Ответил elena20092

Ответ:

V = 1200π

Объяснение:

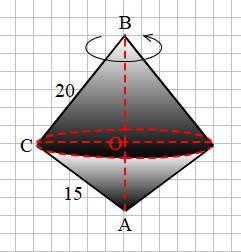
Смотри прикреплённый рисунок.

Прямоугольный ΔАВС с катетами АС = 15 и ВС = 20 вращается вокруг гипотенузы $AB = \sqrt{AC^{2} + BC^{2}}= \sqrt{15^{2} + 20^{2}}= 25.$

Тело вращения представляет собой два конуса с радиусом основания ОС, являющимся высотой, опущенной из вершины прямого угла С на гипотенузу АВ.

$OC = \frac{AC\cdot BC}{AB} = \frac{15\cdot 20}{25}=12.$

Высота верхнего конуса

$BO = \frac{BC^{2} }{AB} = \frac{20^{2} }{25} =16.$

Высота нижнего конуса

$АO = \frac{АC^{2} }{AB} = \frac{15^{2} }{25} =9.$

Объём тела вращения равен

$V = \frac{1}{3}\pi \cdot OC^{2}\cdot BO + \frac{1}{3}\pi \cdot OC^{2}\cdot AO=\\ \\ =\frac{1}{3}\pi \cdot OC^{2}\cdot AB = \frac{1}{3}\pi \cdot 12^{2}\cdot 25 = 1200\pi.$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська література, 1 год назад

невеликий переказ джури козака швайки с 31 по 35 страницу СРОЧНО...

Окружающий мир, 1 год назад

У каких морских животных есть оболочка?

Химия, 1 год назад

Зная соотношения элементов в соединении,составьте его формулу азот и кислород-2:5,натрий азот-3:1,азот и кислород-1:2...

Қазақ тiлi, 1 год назад

Тілі күрмеуге келмеді деген сөзге синоним...

Обществознание, 6 лет назад

2 ЗАДАНИЕ написать вопросы к словам ЦЕННОСТЬ,ОБЩЕСТВО,ЧЕЛОВЕК,ГУМАНИЗМ,СПРАВЕДЛИВОСТЬ ,ПОВЕДЕНИЕ,УВАЖЕНИЕ 3 задание ответьте на вопросы: 1)Возле кокого острова происходили события 2)Каким был...

Математика, 6 лет назад

Тронспортирдің көмегімен 60° бұрышты салыңыз...