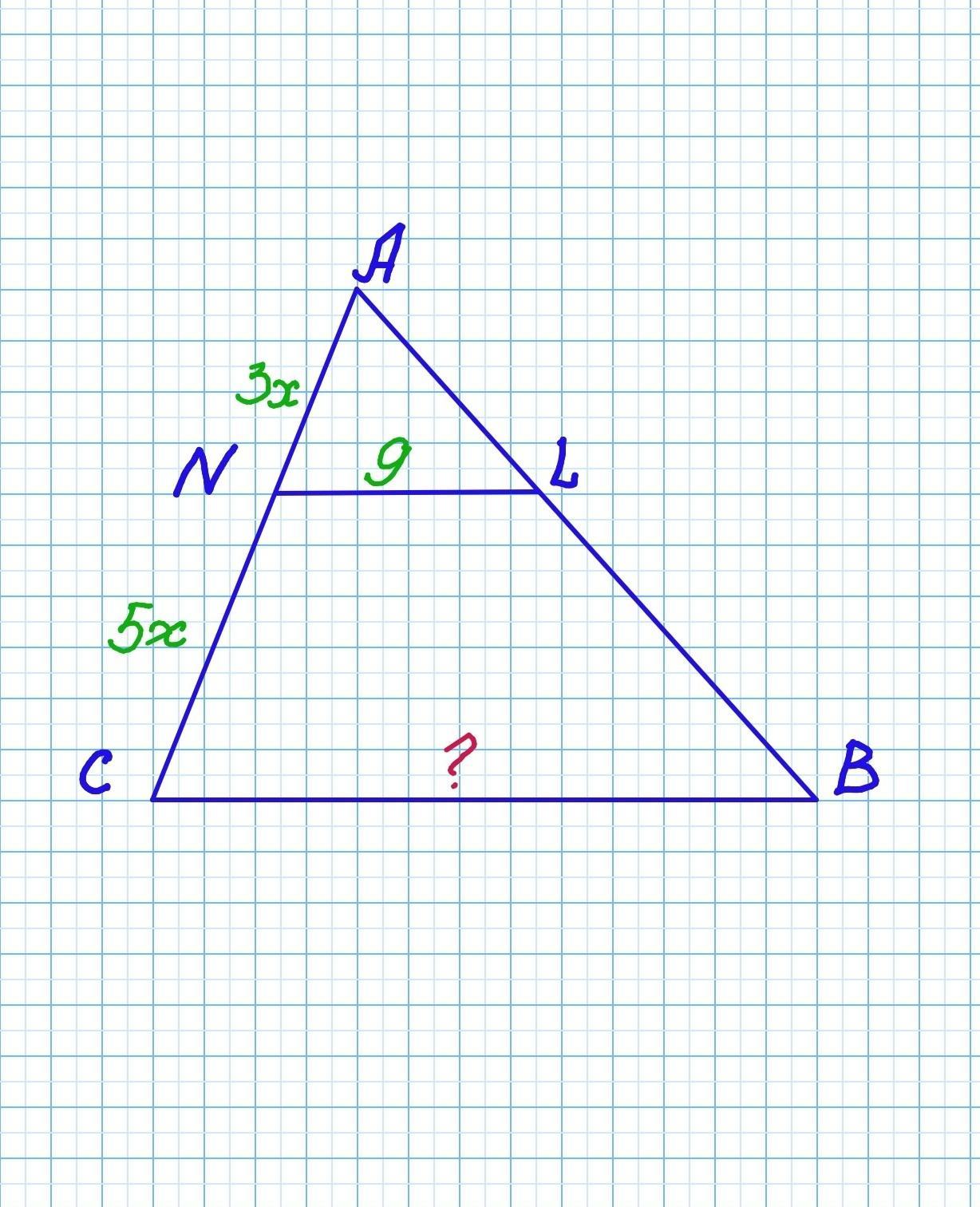
Прямая пересекает стороны АС и АВ треугольника АВС в точках N и L, соответственно, таким образом, что NL параллельна СВ. Известно, что AN : NC = 3 : 5, а сторона NL = 9. Чему равна сторона треугольника СВ?

Прямая пересекает стороны АС и АВ треугольника АВС в точках N и L, соответственно, таким образом, что NL параллельна СВ. Известно, что AN : NC = 3 : 5, а сторона NL = 9. Чему равна сторона треугольника СВ?

Ответ:

СВ=24 ед.

Объяснение:

Рассмотрим △АВС и △АLN.

Так как NL II CB, то ∠ANL=∠ACB -как соответственные углы, образованные при пересечении параллельных прямых секущей АС. ∠A - общий.

△АВС подобен △АLN по двум углам (первый признак подобия треугольников).

Из подобия треугольников следует пропорциональность соответственных сторон:

Так как по условию AN : NC = 3 : 5, то AN=3x, NC=5x, AC=AN+NC=3x+5x=8x.

Тогда:

СВ=24 ед.