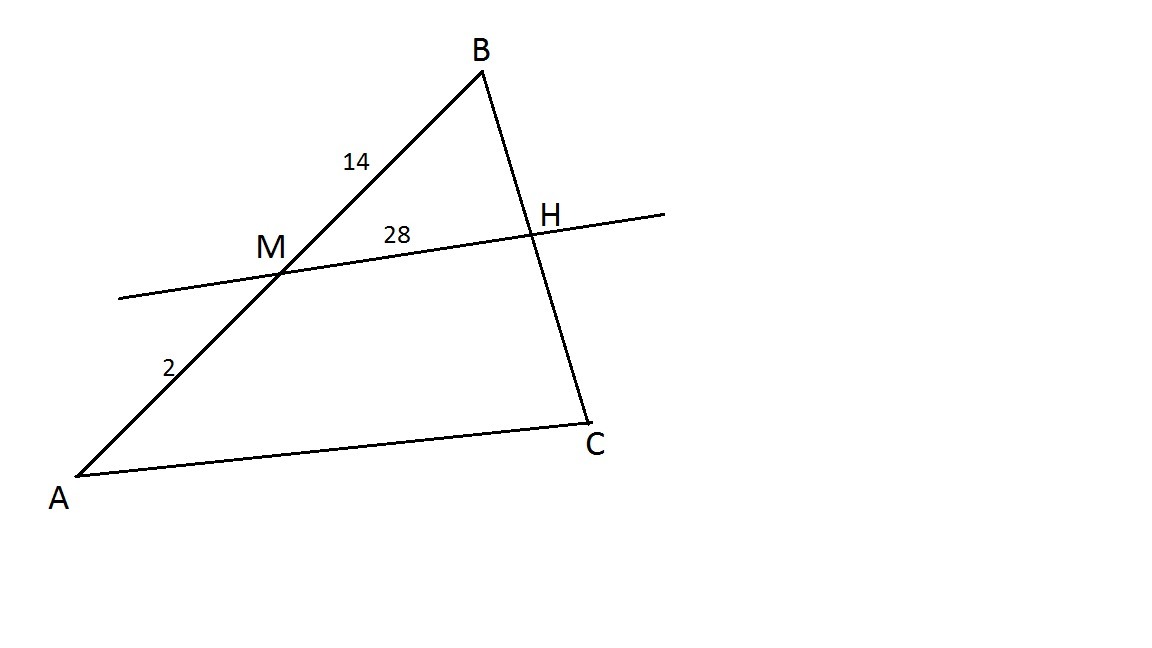
Геометрия, вопрос задал ladafundesh , 8 лет назад

Прямая ,параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС соответственно в точках М и Н.Найдите АС и отношение площадей треугольников АВС и ВМН, если МВ=14 см,АВ=16 см, МН=28 см.

Ответы на вопрос

Ответил Dимасuk

Рассмотрим ΔABC и ΔMBH.
∠BMH = ∠BAC - как соответственные
∠ABC - общий
Значит, ΔMBH~ΔABC - по I признаку.
Из подобия треугольников ⇒
$frac{MB}{AB} = frac{MH}{AC}$
$frac{14}{16} = frac{28}{AC}$ ⇒ $AC = frac{28*16}{14} = 32$ .

Площади треугольников, имеющих равные углы, относятся как произведение сторон, заключающих равные углы.

Тогда $frac{S_M_B_H}{S_A_B_C} = frac{MH*MB}{AB*AC} = frac{28*14}{16*32}= frac{49}{64}$ .

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 2 года назад

268,8:0,56+6,44*12 в столбик!!!

Литература, 2 года назад

Який зміст колискових?

Математика, 8 лет назад

СРОЧНО СРОЧНО СРОЧНО СРООООЧНООО...

Математика, 8 лет назад

У мальчика были друзья у 9 друзей были бананы, 8-апельсины, у 7-сливы У 5 друзей были бананы и апельсины У 3 бананы и сливы У 4 апельсины и сливы У 2 бананы, апельсины и слив Сколько друзей у...

Математика, 9 лет назад

восстановить пропущенные цифры 58( )4-( )( )2( )=3911, 7( )2( )( )-( )8( )34=59085, ( )9( )7( )( )-3( )6( )95=195350,4( )1( )-27( )0=( )571, 561( )8-( )( )28( )=16883, 9( )03( )5-4( )24( )=852( )49.

Литература, 9 лет назад

Сказки каких народов ты читал? Где живут создатели этих сказок? Как отразились особенности жизни этих народов? какие уроки заключены в сказках?