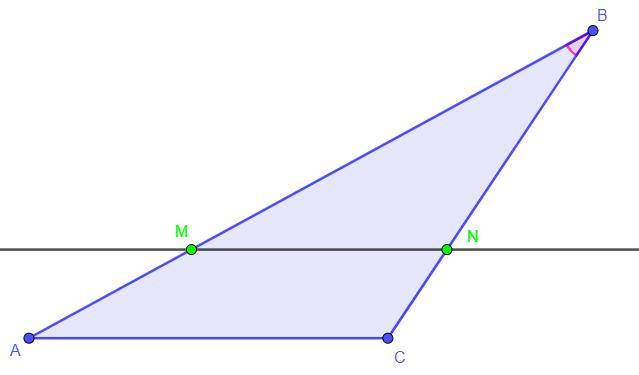
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB = 28, AC = 16, MN = 12. Найдите AM.

Ответ:

AM = 7 см

Объяснение:

Дано: MN║AC, MN ∩ AB = M, MN ∩ BC = N, AB = 28, AC = 16, MN = 12

Найти: AM - ?

Решение:

Треугольник угол ∠ABC - общий, а угол ∠BMN = ∠BAC как соответственные углы при параллельных прямых, так как по условию MN║AC.

Так как треугольник по свойствам подобных треугольников:

см.

По основному свойству отрезка:

AB = AM + MB ⇒ AM = AB - MB = 28 - 21 = 7 см.