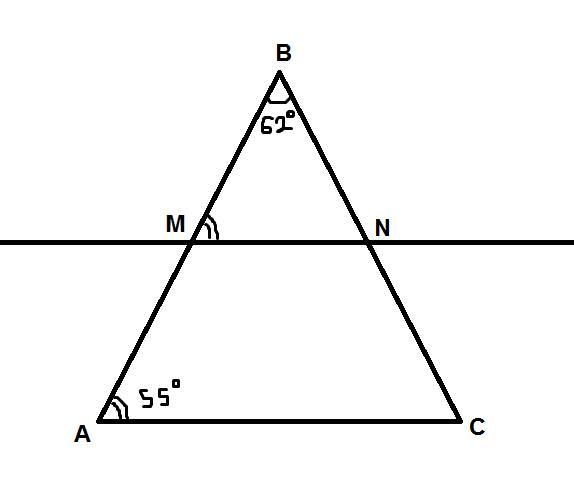
Прямая МN параллельна стороне АС треугольника АВС (точка М лежит на АВ, точка N на BC). Найдите велечину угла BNM , если угол АВС = 62 , угол BAC = 55
Ответы на вопрос
Ответил MynameSvetaSun
0
Решение:
Так как MN║AC, то ∠ВАС=∠BMN=55° как соответственные при пересечении параллельных прямых секущей.
Сумма углов в треугольнике равна 180° ⇒ ∠BMN + ∠MBN + ∠BNM=180°
∠BMN=55°, ∠ABC=∠MBN=62° ⇒
∠BNM=180° - 55° - 62°=180° - 117°=63°
Ответ: 63°
Приложения:
Ответил zhambyl76
0
Центрі у=х+2 түзуінің бойында жататын және А(3; 0); В(-1; 2) нүктелері арқылы өтетін шеңбердің теңдеуін табыңыз.
Ответил zhambyl76
0
Мына есепті қарап жібере аласыз ба
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Биология,
7 лет назад
Математика,
7 лет назад
Математика,
8 лет назад