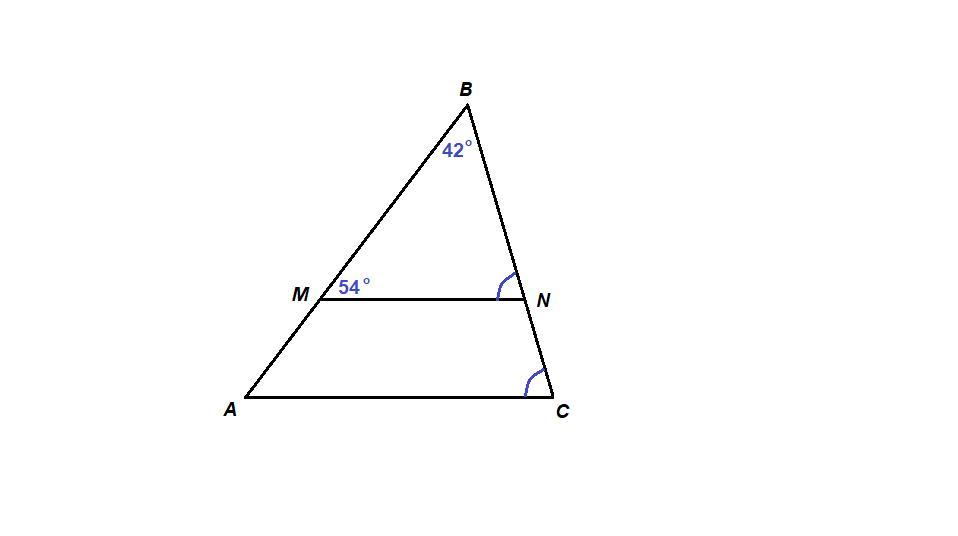
Прямая MN параллельна стороне AC треугольника ABC(точка M лежит на AB,точка N-на BC).Найдите величину угла ACB,если угол ABC=42°,угол BMN=54°​

Ответ:

Пошаговое объяснение:

Так как прямая MN параллельна стороне АС, то тогда угол BMN равен углу BAC, а угол BNM равен углу ACB. Сумма углов в треугольнике равна 180 градусов. Значит угол ACB=180-ABC-BAC=180-42-54=84.

Ответ: угол ACB= 84 градуса.

Ответ:  84°

Пошаговое объяснение:

Сумма углов треугольника равна 180°.

Из ΔMBN:

∠MNB = 180° - (∠BMN + ∠MBN) = 180° - (54° + 42°) = 180° - 96° = 84°

∠ACB = ∠MNB = 84° как соответственные при пересечении параллельных прямых MN и АС секущей ВС.