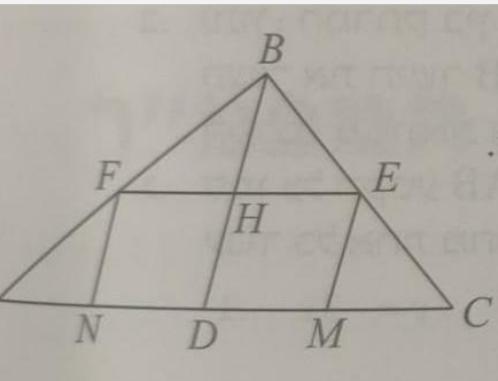
Прямая BD медиана к гипотенузе прямоугольного треугольника ABC. FM и EM это серединные линии в треугольниках BCD ABD соответственно.
1. Доказать что EHDM это ромб.
2. Дано: AB = 16 BC = 12 узнайте периметр ромба EHDM
Приложения:
avladimirov0906:
Не FM а FN
Ответы на вопрос
Ответил anastasiapff
1
Ответ:
1
BD=1/2AC=DC => треугольник ВDC - равнобедренный
ЕМ - средняя линия => ЕМ=1/2ВD
EM - средняя линия => ВН=HD
по т. Фалеса ВЕ=ЕС => EH - средняя линия и EH=1/2DC
BD=DC => EH=EM
средние линии параллельны основаниям треугольников => ЕМ || ВD и ЕН || DC => DHEM - параллелограмм => НD=EM и НЕ=DM, а ЕН=ЕМ => НD=EM=НЕ=DM => это ромб
2
по теореме Пифагора
АС²=АВ²+ВС²
АС²=16²+12²=256+144=400
АС=20
BD=1/2AC (из доказательства 1) => BD=1/2*20=10
BH=HD (из доказательства 1) => HD=1/2BD=1/2*10=5
Phdme=HD+DM+ME+HE=4HD (т.к. НDME - ромб)
Phdme=4*5=20
Новые вопросы