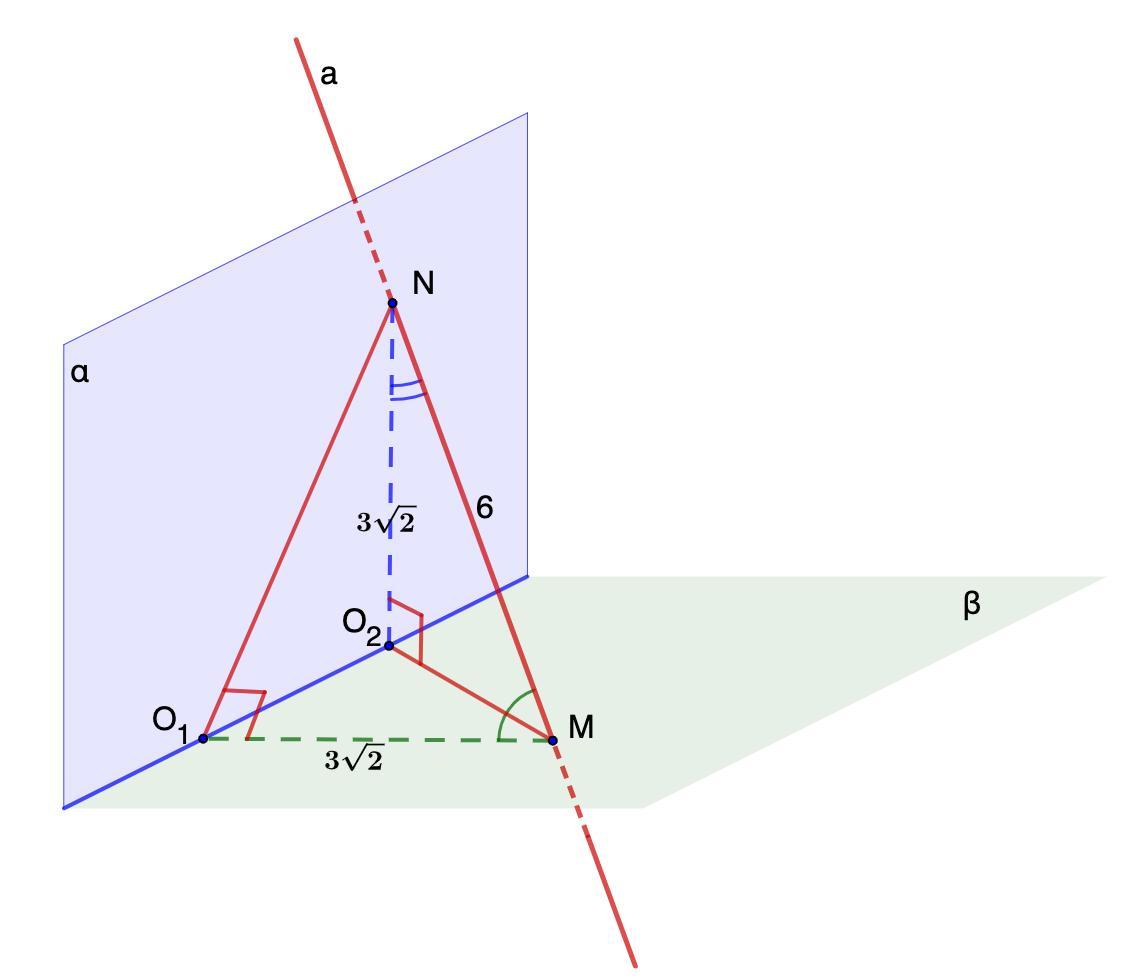
Прямая а пересекает перпендикулярные друг другу плоскости в точках Ми N. Расстояния от этих точек до линии пересечений плоскостей: мо1, — 3 корень 2 и NO2, = 3 корень 2, где 01 и O2, — точки, лежащие на линии пересечения плоскостей. Длина отрезка MN равна 6. Найдите углы, которые отрезок MN образуют с данными плоскостями. Укажите величину угла NMO1 в градусах. Укажите величину угла MNO2, в градусах.

Ответ:

Величина угла NMO₁ равна 45°, величина угла MNO₂ равна 45°.

Объяснение:

Требуется указать величину угла NMO₁ в градусах, указать величину угла MNO₂ в градусах.

Дано: α ⊥ β;

а ∩ α = N; a ∩ β = M;

MO₁ = 3√2; NO₂ = 3√2 - расстояния от М и N до О₁О₂ - линии пересечения плоскостей.

МN = 6.

Найти: ∠NMO₁  и ∠MNO₂.

Решение:

1. Рассмотрим ΔО₁NM.

• Расстояние от точки до прямой - перпендикуляр, опущенный из точки на данную прямую.

⇒ МО₁ ⊥ О₁О₂

• Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна второй плоскости.

⇒ МО₁ ⊥ α

• Если прямая перпендикулярна к плоскости, то она перпендикулярна любым прямым, лежащим в этой плоскости.

⇒ МО₁ ⊥ O₁N

ΔО₁NM - прямоугольный.

MO₁ = 3√2;  МN = 6.

2. Рассмотрим ΔO₂MN.

Аналогично п.1:

NO₂ ⊥ O₁O₂

NO₂ ⊥ β

NO₂ ⊥ O₂M

⇒ ΔO₂MN - прямоугольный.

∠NMO₁  = ∠MNO₂ = 45°