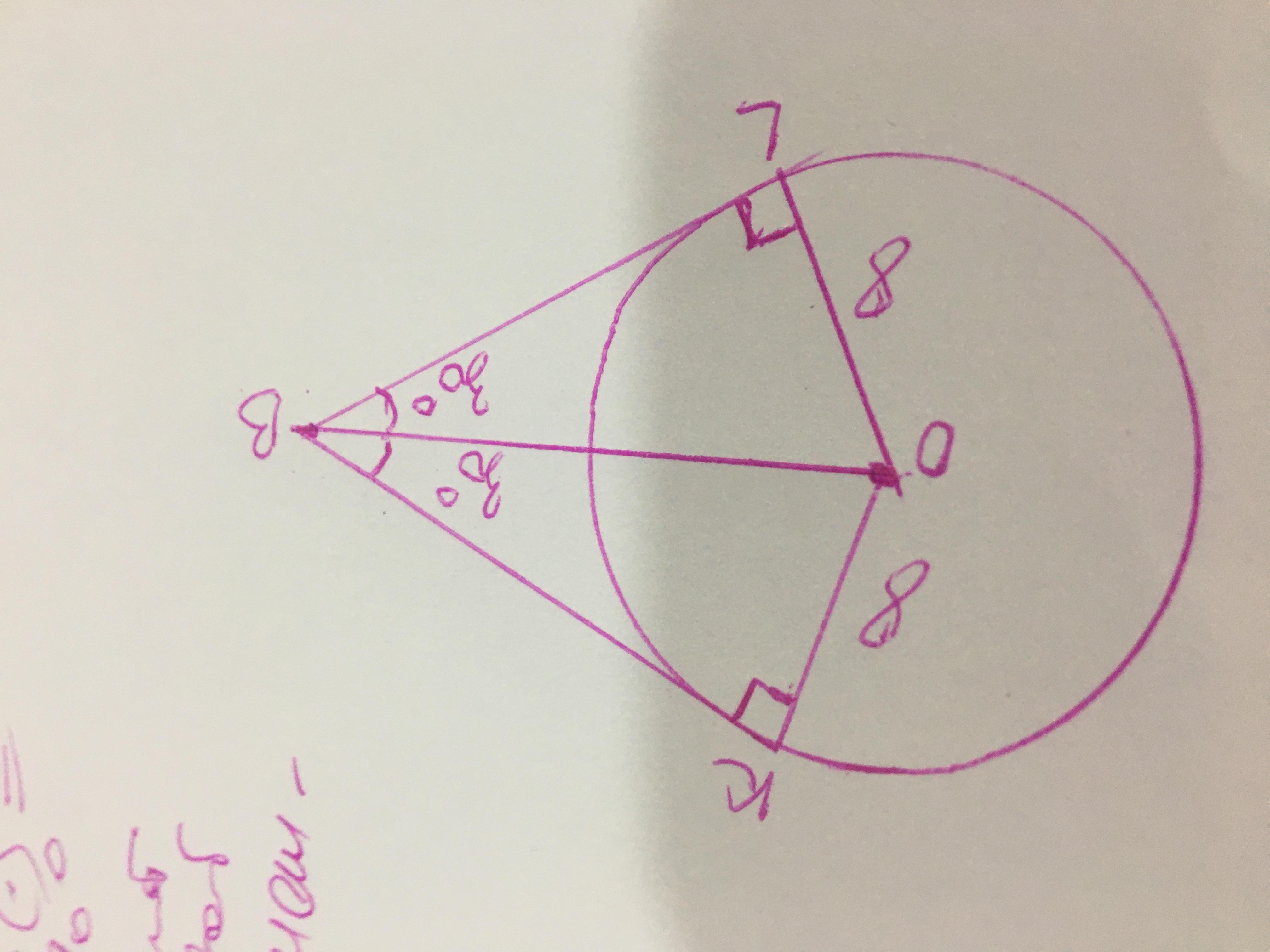
Прямі BK і BL дотикаються до кола із центром О в точках K і L, ∠KBL = 60°. Знайди довжину відрізка BО, якщо радіус кола дорівнює 8 см.
Ответы на вопрос
Відповідь:
Ми знаємо, що радіус кола дорівнює 8 см, і ∠KBL = 60°.
Оскільки прямі BK і BL дотикаються до кола, вони є перпендикулярними до радіуса, проведеного в точці дотику. Тобто, ∠BKO і ∠BLO є прямими кутами.
Зараз ми маємо прямокутний трикутник BKO, де ОК - радіус кола, а BK - відрізок, який ми хочемо знайти.
Ми знаємо, що у прямокутних трикутниках співвідношення між катетами і гіпотенузою дається теоремою Піфагора:
BK² + KO² = BO².
Де BK - відрізок, який ми шукаємо (BО), KO - радіус кола (8 см), і BO - гіпотенуза.
Також, ми знаємо, що у нас є прямий кут в точці О (BO - радіус кола і BK - пряма, яка дотикається до кола). Тобто, ми можемо використовувати теорему Піфагора для цього трикутника.
BO² = BK² + KO²,
BO² = BK² + (8 см)²,
BO² = BK² + 64 см².
Тепер нам відомо, що ∠KBO - прямий кут, і ∠KBL = 60°. Отже, ∠KBO = 90° - 60° = 30°.
Ми знаємо, що в прямокутних трикутниках, тангенс кута дорівнює відношенню протилежного катета до прилеглого катета:
tan(∠KBO) = KO / BK,
tan(30°) = 8 см / BK.
Тепер ми можемо знайти BK:
tan(30°) = 1/√3.
Тепер ми можемо розв'язати рівняння для BK:
BK = 8 см / (1/√3) = 8√3 см.
Отже, довжина відрізка BО дорівнює 8√3 см.
Ответ:
Отрезки касательных,которые проведены из одной точки,равны
KB=BL
Касательные и радиусы взаимно перпендикулярны,поэтому
<ОКВ=<ОLB=90*
Прямая ОВ,проложенная из стартовой точки В до центра,делит угол между касательными пополам
<КАО=<LBO=<KBL:2=60:2=30*
Образовались два равных прямоугольных треугольника(по 4 признаку равенства прямоугольных треугольников-по катету и гипотенузе)
Рассмотрим один из них
Треугольник ОВL
Он прямоугольный
<ОLB=90*
Катет ОL лежит напротив угла 30* (<ОВL=30*),a это значит,что гипотенуза ОВ в два раза больше катета ОL
OB=OL•2=8•2=16 см
Объяснение: