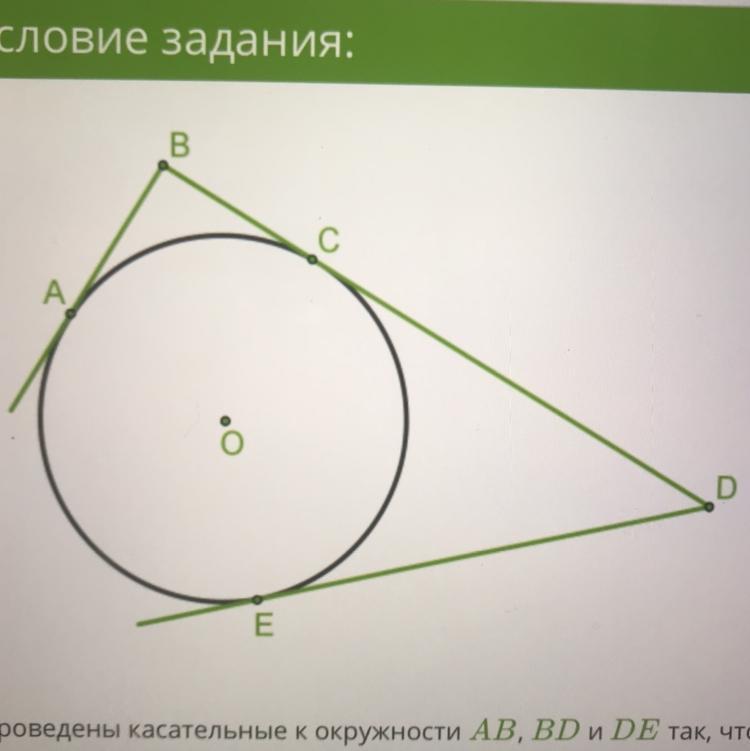
Проведены касательные к окружности AB, BD и DE так, что A, C и E - точки касания. Длина ломаной ABDE равна 5,1 см. Определи длину отрезка DB.

Ответ:

2,55

Объяснение:

AB+BC+CD+DE=5,1

Т.к. , AB=BC, CD=DE, то

BC+BC+CD+CD=5,1

2BC+2CD=5,1

BC+CD=5,1/2

BD=2,55

Ответ:

Объяснение:

Из свойства двух касательных  окружности следует. что

АВ=ВС и СД=ДЕ.

Пусть АС=ВС=х, тогда СД=ДЕ=у

АЕ=2х+2у=2(х+у)=5,1

х+у=5.1:2

х+у=2,55, ВД=ВС+СД=х+у=2,55см

ВД=2,55см