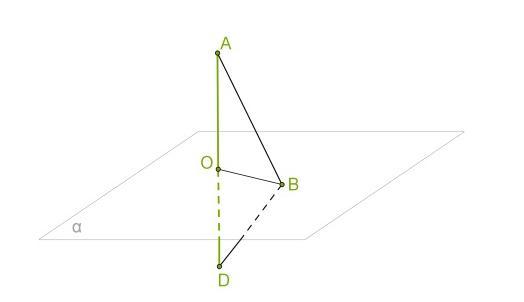
Проведённая к плоскости перпендикулярная прямая пересекает плоскость в точке О. На прямой отложен отрезок АD), точка О является серединной точкой этого отрезка. Определи вид и периметр треугольника АВD, если АD = 11 см, а ОВ = 5 см (ответ округли до одной

десятой).

Проведённая к плоскости перпендикулярная прямая пересекает плоскость в точке О. На прямой отложен отрезок АD), точка О является серединной точкой этого отрезка. Определи вид и периметр Δ АВD, если АD = 11 см, а ОВ = 5 см (ответ округли до одной  десятой).

Объяснение:

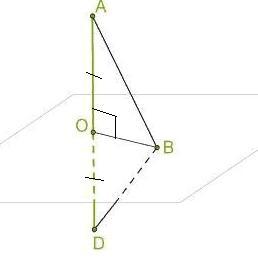
1) ΔАОВ=ΔDOB  как прямоугольные (ВО⊥AD) по двум катетам :ВО=DО=5,5 ,BO-общий  ⇒ AB=DB  ⇒Δ АВD равнобедренный .

2)Найдем боковые стороны из ΔАОВ-прямоугольного по т. Пифагора АВ=√(5,5²+5²)=√55,25≈5,43≈5,4  .