Прошу помогите срочно решить квадратные уравнение
1. 4x²+8=0
2. x²-x-2=0
3. 2x²+10x=0
4. x²+2x-8=0
(Нужно чтобы вы написали сколько корней, есть ли он вообще!
И ещё, обязательно с фото в тетради, решите с формулой D=b²-4ac после этого используйте формулу x¹'²=-b±√D/2a
Если корней нет, то 2ую формулу не пишите, просто напишите что нету корней и все! СРОЧНО! ОБЯЗАТЕЛЬНО С ФОТО НА ЛИСТОЧКЕ ПРОШУ
Ответы на вопрос
Ответ:
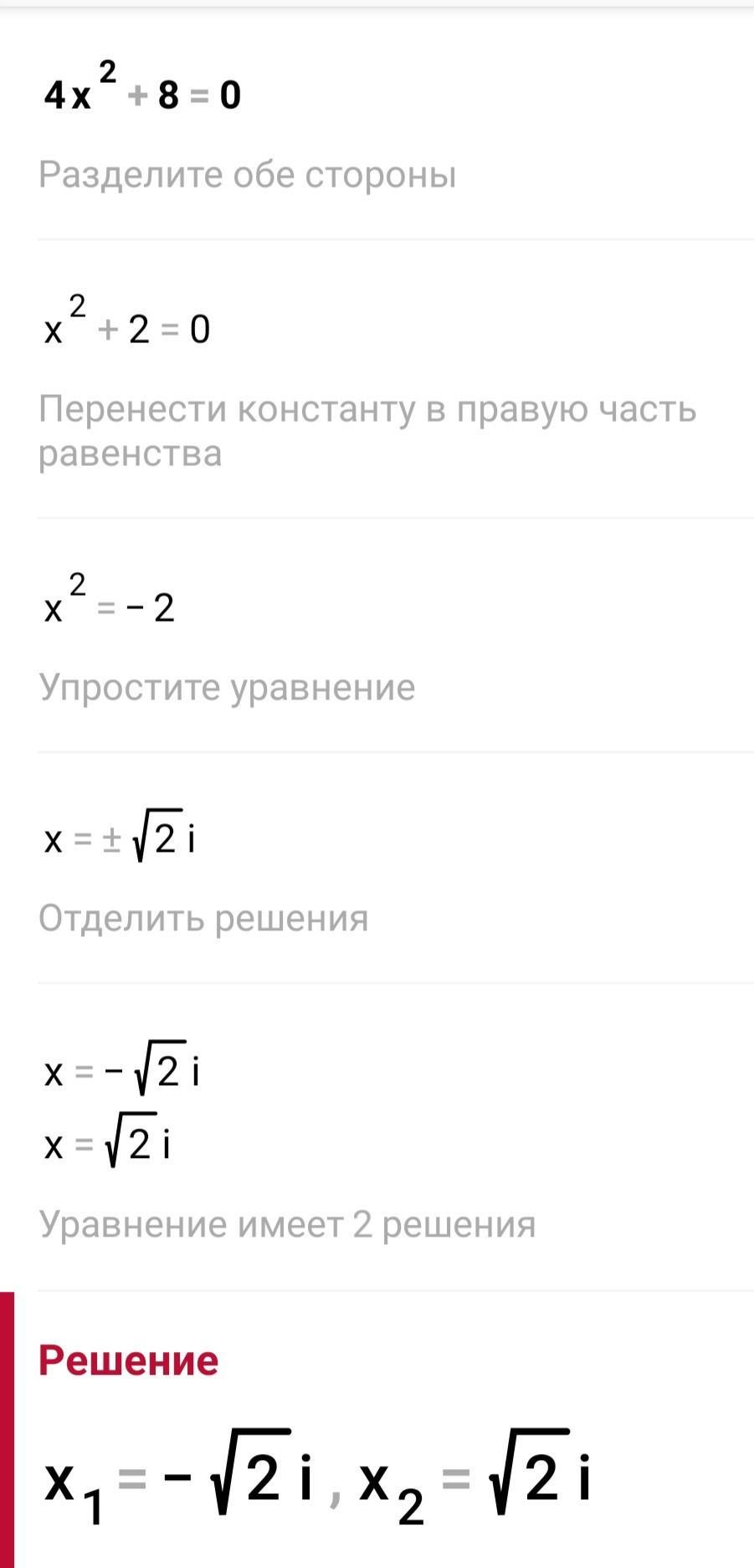
1. 4x²+8=0
Для того, чтобы решить это уравнение, сначала нужно вынести общий множитель:
4x²+8 = 4(x²+2) = 0
Затем используем свойство произведения, которое гласит, что произведение равно нулю только тогда, когда хотя бы один из множителей равен нулю:
4(x²+2) = 0
x²+2 = 0
x² = -2
Уравнение не имеет решений в действительных числах, так как квадрат любого действительного числа не может быть отрицательным. Таким образом, это уравнение не имеет действительных корней.
2. x²-x-2=0
Решим это квадратное уравнение, используя формулу дискриминанта:
D = b² - 4ac
где a = 1, b = -1, и c = -2.
D = (-1)² - 4(1)(-2) = 1 + 8 = 9
D > 0, поэтому у уравнения два корня:
x1 = (-b + √D)/2a = (1 + 3)/2 = 2
x2 = (-b - √D)/2a = (1 - 3)/2 = -1
Ответ: x1=2, x2=-1
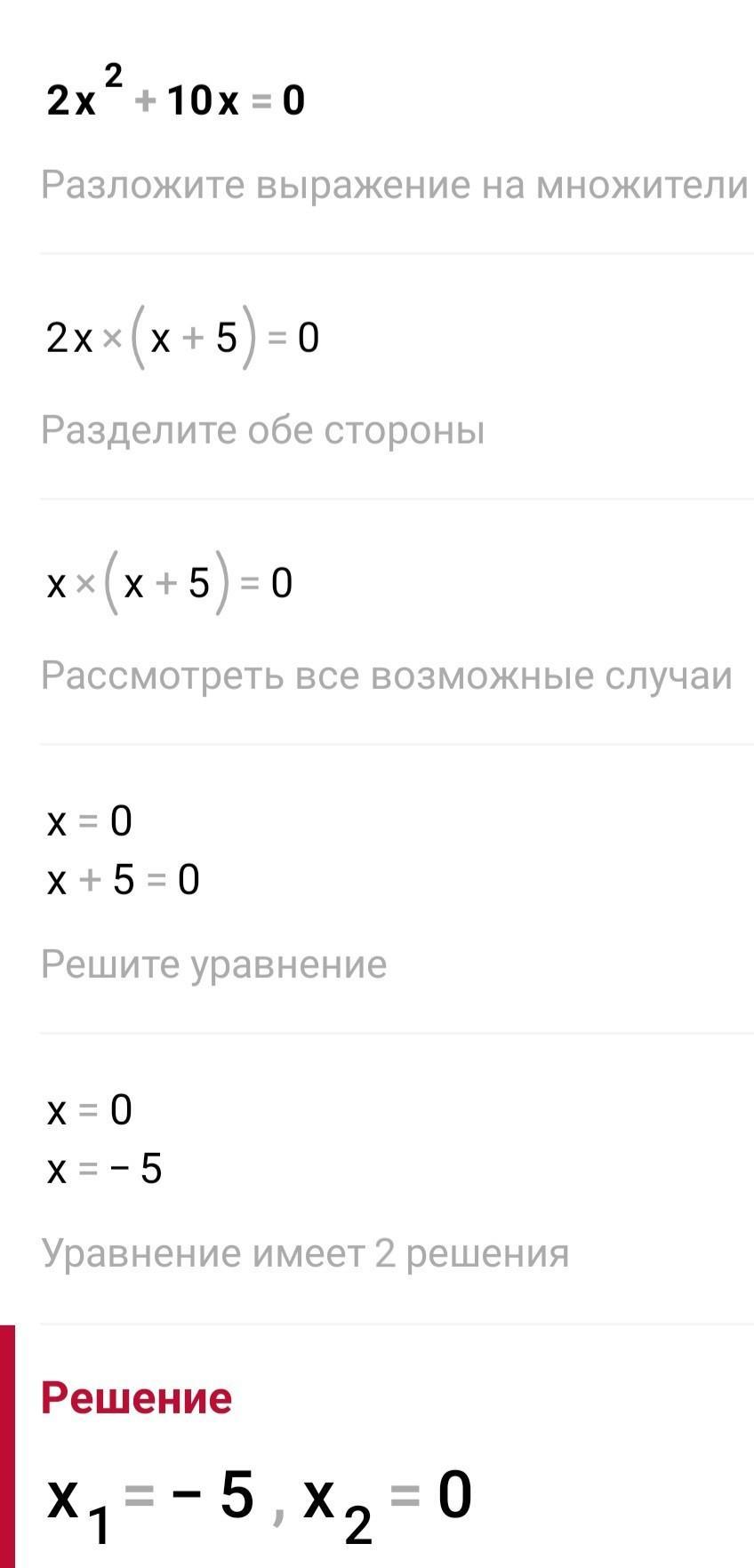
3. 2x²+10x=0
Для того, чтобы решить это уравнение, сначала нужно вынести общий множитель:
2x(x+5) = 0
Затем используем свойство произведения, которое гласит, что произведение равно нулю только тогда, когда хотя бы один из множителей равен нулю:
2x=0 или x+5=0
Отсюда x=0, x=-5. Уравнение имеет два корня: x=0, x=-5
4. x²+2x-8=0
Решим это квадратное уравнение, используя формулу дискриминанта:
D = b² - 4ac
где a = 1, b = 2, и c = -8.
D = 2² - 4(1)(-8) = 4 + 32 = 36
D > 0, поэтому у уравнения два корня:
x1 = (-b + √D)/2a = (-2 + 6)/2 = 2
x2 = (-b - √D)/2a = (-2 - 6)/2 = -4
Ответ: x1=2, x2=-4
Ответ:
смотри на фото
Объяснение:
можешь пж сделать лучшим