Алгебра, вопрос задал ANITA4568 , 6 лет назад

Прошу помогите!!
Решите два задания:

Приложения:

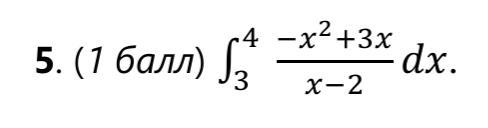
Ответы на вопрос

Ответил NNNLLL54

Ответ:

$1)\ \ y=2x-x^2\ ,\ y=0\ ,\ M(\, \frac{1}{2}\, ;\, \frac{3}{4}\, )$

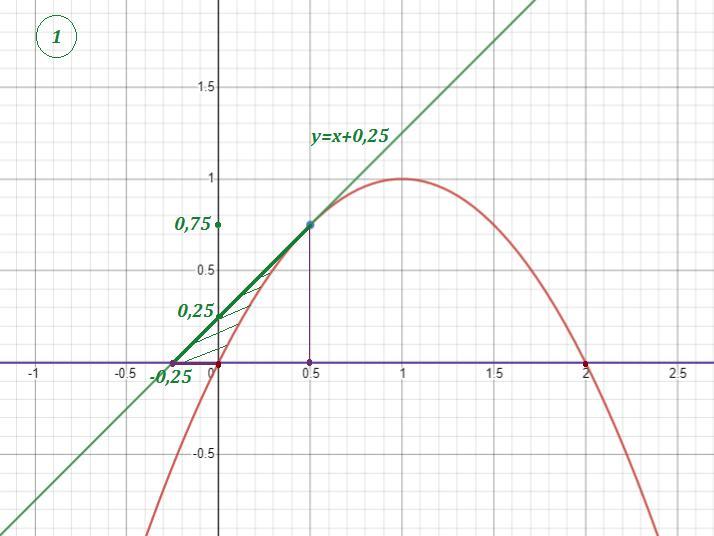
Составим уравнение касательной к параболе в точке М.

$y'(x)=2-2x\ \ ,\ \ y'(\dfrac{1}{2})=y'(0,5)=2-1=1\ \ \to \ \ k=1\\\\y(\dfrac{1}{2})=y(0,5)=2\cdot\dfrac{1}{2}-\dfrac{1}{4}=\dfrac{3}{4}=0,75\\\\y=0,75+1\cdot (x-0,5)\ \ \ \to \ \ \ \ \underline{\ y=x+0,25\ }\ \ -\ kasatelnaya$

Точка пересечения касательной с ОХ - это точка $(-0,25\ ,\ 0\ )$ .

Точки пересечения параболы с ОХ:

$2x-x^2=0\ \ ,\ \ x(2-x)=0\ ,\ x_1=0\ ,\ x_2=2$

$\displaystyle S=\int\limits_{-0,25}^{0,5}(x+0,25)\, dx-\int\limits_0^{0,5}(2x-x^2)\, dx=\Big(\dfrac{x^2}{2}+0,25x\Big)\Big|_{-0,25}^{0,5}-\Big(x^2-\frac{x^3}{3}\Big)\Big|_0^{0,5}=\\\\\\=\frac{0,25}{2}+0,125-\frac{0,0625}{2}+0,0625-0,25+\frac{0,125}{3}=\frac{0,0625}{2}+\frac{0,125}{3}=\\\\\\=\frac{1}{32}+\frac{1}{24}=\frac{7}{96}$

$\displaystyle 2)\ \int\limits^4_3\frac{-x^2+3x}{x-2}\, dx=\int\limits^4_3\Big(-x+1+\frac{2}{x-2}\Big)\, dx=\Big(-\frac{x^2}{2}+x+2\, ln|x-2|\Big)\Big|_3^4=\\\\\\=-\frac{16}{3}+4-2\, ln2+\frac{9}{2}-3-2\, ln1=-\frac{1}{6}-2\, ln2$