Прошу, помогите~!!! ​Даю 70 баллов

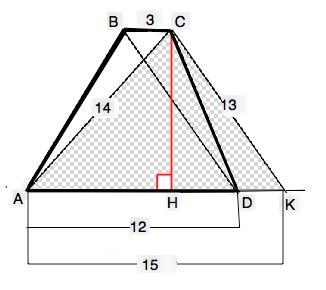
   Найдите площадь трапеции, у которой основания равны 3 см и 12 см, а диагонали – 13 см и 14 см.

Ответ: 84 см²

Объяснение: Сделаем рисунок к задаче и обозначим трапецию  АВСD (ВС||AD, ВС< AD). Из вершины C параллельно диагонали ВD проведем прямую до пересечения с продолжением AD в точке К и получим треугольник АСК со сторонами АС=14 см, СК=ВD=13 см, и АК=АD+DK=12+3=15 cм, (DK=BC так как DBCK- параллелограмм по построению),

Площадь трапеции равна половине произведения суммы оснований на высоту.

Площадь треугольника АСК равна  Высота у трапеции и треугольника АСК общая. Следовательно, площадь трапеции ABCD равна площади ∆ АСК.

Найдем площадь ∆ АСК по формуле Герона.

р∆(АСК)=(14+13+15):2=42:2=21

Ѕ(АСК)=√21•(21-14)21-13)(21-15)=84 см² ⇒

Ѕ(ABCD)=84 см²