Математика, вопрос задал apels6in , 2 года назад

Производные Производные срочно

Приложения:

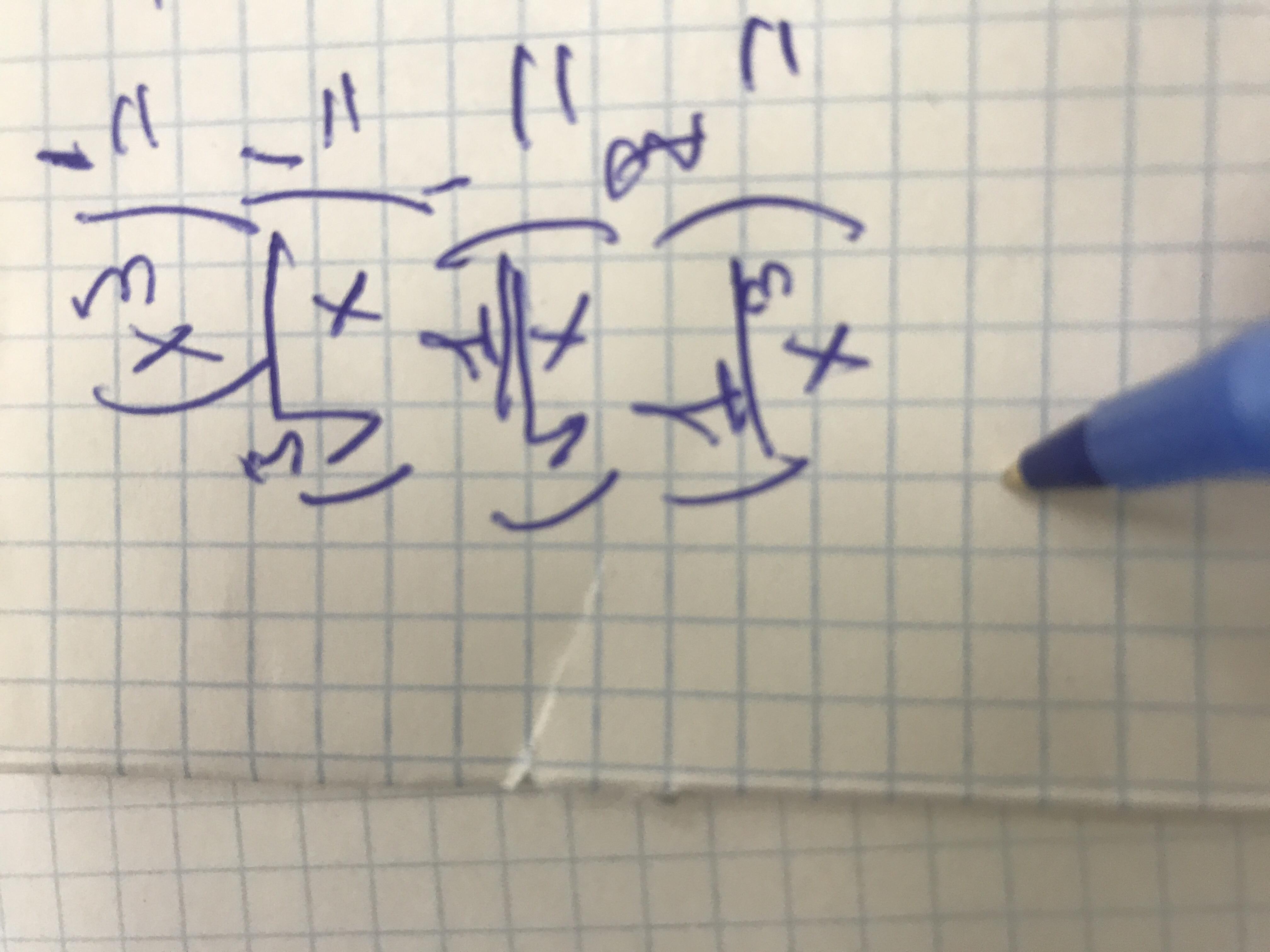
Ответы на вопрос

Ответил Miroslava227

1

Ответ:

$( {x}^{3} )' = 3 {x}^{2}$

$( \sqrt[3]{x} ) '= ( {x}^{ \frac{1}{3} } ) '= \frac{1}{3} {x}^{ - \frac{2}{3} } = \frac{1}{3 \sqrt[3]{ {x}^{2} } } \\$

$( \frac{1}{ \sqrt{x} } )' = ( {x}^{ - \frac{1}{2} } ) '= - \frac{1}{2} {x}^{ - \frac{3}{2} } = - \frac{1}{2x \sqrt{x} } \\$

$( \frac{1}{ {x}^{3} } ) '= ( {x}^{ - 3}) '= - 3 {x}^{ - 4} = - \frac{3}{ {x}^{4} } \\$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

1)В чём отличие предложения от словосочетания ?2)На какие две группы делятся предложения по количеству грамматических основ ?3)Из чего состоит грамматическая основа двусоставного простого предложения...

Русский язык, 1 год назад

Слова тень,день,бровь,червь и др выписать сначала имя сущ. 3 склонения потом 2 скл...

Физика, 2 года назад

СРОЧНО!!! Помогите!!! В сообщающихся сосудах находятся ртуть, вода и керосин. Определи высоту каждого слоя жидкости.

Математика, 2 года назад

реши уравнения. проверь.

География, 7 лет назад

Первооткрыватель Васко да Гама. Реферат не большой.

История, 7 лет назад

при котором российском императоре история была выделена в отдельную науку: Петра 1 Александра 1 Александра 2 Катерины 2...