Производные функции
Заранее спасибо
Приложения:
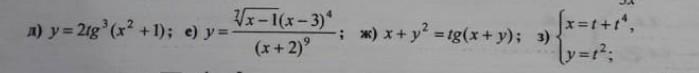
Ответы на вопрос
Ответил NNNLLL54
1
Ответ:
Dv1ishnik:
Если не секрет, где вы так красиво заполняете примеры
а последний пример у вас не получился
использую редактор формул LaTex ... а что не получилось ?
4 пример з)
всё там правильно, формула для производной параметрически заданной функции используется
У меня какие то команды там
это команды из редактора формул...значит они у вас почему-то не преобразуются в нормальный текст. попробуйте перезагрузить страницу не с телефона.
Ок только завтра утром
С покойной ночи
Новые вопросы