Математика, вопрос задал miniwars56655 , 6 лет назад

Продифференцировать данную функцию!

Приложения:

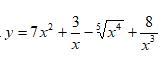
mlanshychumakov: я непайму что нужно найти

mlanshychumakov: найти пересечение с осью у

mlanshychumakov: или найти область определения

mlanshychumakov: или

mlanshychumakov: найти производную

mlanshychumakov: или

mlanshychumakov: найти вертикальные асимпоты

mlanshychumakov: или определить чётные или нечётные ?

Ответы на вопрос

Ответил mlanshychumakov

$y = 7x {}^{2} + \frac{3}{x} - \sqrt[5]{x {}^{4} } + \frac{8}{x {}^{3} }$

$y = \frac{d}{dx} (7x {}^{2} + \frac{3}{ {x}^{} } - \sqrt[5]{x {}^{4} } + \frac{8}{x {}^{3} } )$

$y = \frac{d}{dx} (7x {}^{2} + \frac{3}{ {x}^{} } -x {}^{ \frac{4}{5} } + \frac{8}{x {}^{3} } )$

$y = \frac{d}{xd} (7x {}^{2} ) + \frac{d}{dx} ( \frac{3}{x} ) - \frac{d}{dx} {}{(x ^\frac{4}{5} )} + \frac{d}{dx} ( \frac{8}{x {}^{3} } )$

$y = 7 \times 2x - 3 \times \frac{1}{x {}^{2} } - \frac{4}{5} x {}^{ - \frac{1}{5} } - 8 \times \frac{3x {}^{2} }{(x {}^{3} ) {}^{2} }$

$y {}^{1} = 14x - \frac{3}{x {}^{2} } - \frac{4}{5 \sqrt[5]{x} } - \frac{24}{x {}^{4} }$

Новые вопросы

Русский язык, 1 год назад

Русский язык, 1 год назад

История, 6 лет назад