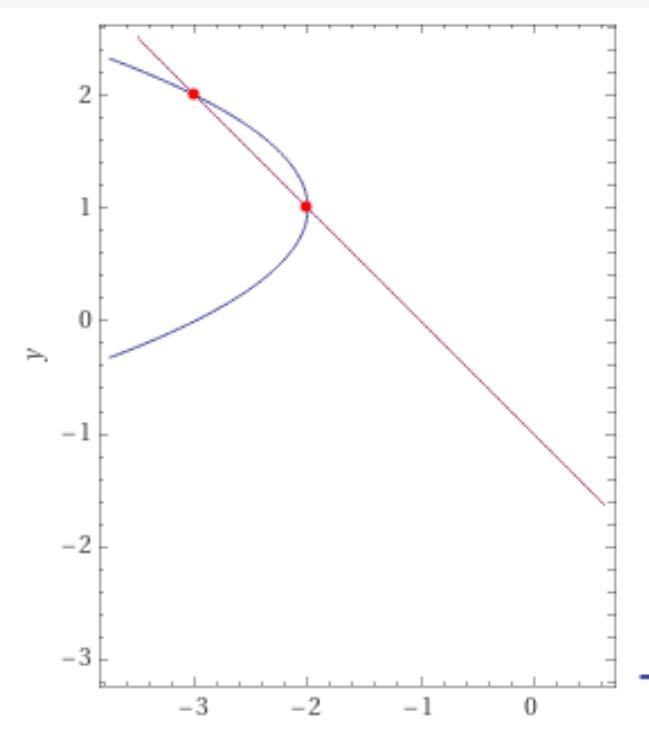
Привести уравнение кривой второго порядка f(х,у)=0 к каноническому виду и найти точки пересечения ее с прямой Ах+Ву+С=0
х + у ²- 2у + 3 = 0, х + у + 1 = 0
Ответы на вопрос
Даны уравнения кривой х + у ²- 2у + 3 = 0 и прямой х + у + 1 = 0.
1) В уравнении кривой выделяем полные квадраты:
(y²-2·1y + 1) -1·1 = (y-1)²-1 .
Преобразуем исходное уравнение:
(y-1)² = -x -2 .
Получили уравнение параболы:
(y - y0)² = 2p(x - x0) ,
(y-1)² = 2·(-1/2)(x - (-2)) .
Ветви параболы направлены влево, вершина расположена в точке (x0, y0), то есть в точке (-2;1) .
Параметр p = (-1/2 )
Координаты фокуса: F((xo + (p/2)); yo) = ((-2 - (1/4)); 1) =( (-9/4);1).
Уравнение директрисы: x = x0 - p/2
x = -2 - (-1/4) = (-7/4 ).
2) Координаты точек пересечения находим совместным решением уравнений кривой и прямой.
х + у ²- 2у + 3 = х + у + 1 ,
у ²- 3у + 2 = 0, Д = 9 - 4*1*2 = 1, у1 = (3 - 1)/2 = 1, у2 = (3 + 1)/2 = 2.
х1 = -у - 1 = -1 - 1 = -2, х2 = -2 - 1 = -3.