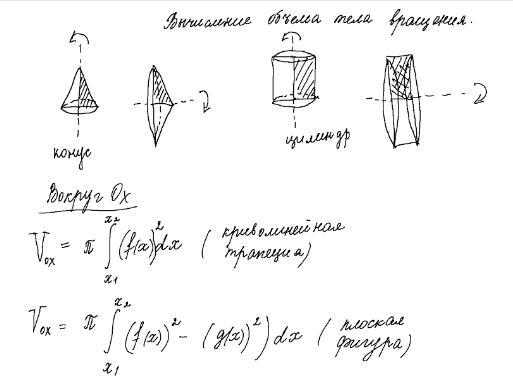
Алгебра, вопрос задал shvyryaev03 , 2 года назад

Применение вычисления интегралов. Вычислите объем тела вращения.
y=4x-x^2
y=0

Приложения:

Ответы на вопрос

Ответил olgaua64
1

Ответ:

V=\pi \int\limits^4_0 {(4x-x^2)}^2 \, dx

V=\pi \int\limits^4_0 {(4x-x^2)}^2 \, dx=\pi \int\limits^4_0 {(16x^2-8x^3+x^4)} \, dx

=16/3 x^3 -8/4 x^4 +1/5 x^5 |^4_0= 16/3*64-2*256+ 1/5*1024=34,1333*\pi

Объяснение:

4x-x^2=0

x=0  x=4

shvyryaev03: это площадь, а нужен объем
olgaua64: умножаем на \пи имеем обьем фигури вращения
olgaua64: нужно брать квадрат функции
olgaua64: все
Ответил sangers1959
1

Объяснение:

y=4x-x^2\ \ \ \ y=0\ \ \ \ \ V=?\\4x-x^2=0\\x*(4-x)=0\\x_1=0\\4-x=0\\x_2=4.\\V=\pi *\int\limits^4_0 {(4x-x^2)^2} \, dx=\pi *\int\limits^4_0 {(16x^2-8x^3+x^4)} \, dx=\\=\pi *(\int\limits^4_0 {16x^2} \, dx -\int\limits^4_0 {8x^3} \, dx +\int\limits^4_0 {x^4 \, dx)=\pi *(16*\int\limits^4_0 {x^2} \, dx -8*\int\limits^4_0 {x^3} \, dx +\int\limits^4_0 {x^4 \, dx)=

=\pi *(16*\frac{x^3}{3}\ |_0^4-8*\frac{x^4}{4}\ |_0^4+\frac{x^5}{5}\ |_0^4)=\pi *(16*\frac{4^3}{3} -2*4^4+\frac{4^5}{5})=\\=\pi *(\frac{16*64}{3}-2*256+\frac{1024}{5})=\pi *(\frac{1024}{3} -512 +\frac{1024}{5})=\pi *(\frac{5*1024+3*1024}{3*5}-512)=\\=\pi *(\frac{1024*(5+3)}{15} -512)=\pi *(\frac{1024*8}{15} -512)=\pi *(\frac{8192}{15}-512)=\\=\pi *\frac{8192-512*15}{15}= \pi *\frac{8192-7680}{15}=\frac{512\pi }{15}\approx107,233.

Ответ: V≈107.233 куб. ед.

shvyryaev03: Спасибо Вам огромное. Если вам не сложно, могли бы ли Вы решить еще вот эту задачу. Если решите, то заранее спасибо большое. https://znanija.com/task/40987625
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Русский язык, 1 год назад
Укажите неверное утверждение: 1) односоставное предложение может быть распространённым 2) определённо-личные предложения имеют один главный член предложения - сказуемое 3)безличными называются...
Английский язык, 1 год назад
Помогите пожайлуста с английским буду очень благодарна. Ask and answer, as in the example. 2) they/fish?  3) the girl/read a magazine?  4) they /listen to music?  5) boys/ wear trousers?  6) the...
Математика, 2 года назад
Запиши множества решений неравенства 343< или = X <396 делителями которых являются 2 и 9...
Биология, 2 года назад
У деяких дієтах з раціону людини виключаються певні компоненти, наприклад жири. Чи можуть виникнути в людини, яка дотримується такої дієти, проблеми зі здоровям? Чому?
Геометрия, 7 лет назад
Найдите углы прямоугольно трапеции если один из углов равен 130 гдасов...
Литература, 7 лет назад
кто герой сидел под образом в красном кафтане в высокой шапке и важно подбочасть...