При яких значеннях параметра а рівняння (27- х^3)/(х-3)= а має корені та скільки?

Ответ:

(см. объяснение)

Объяснение:

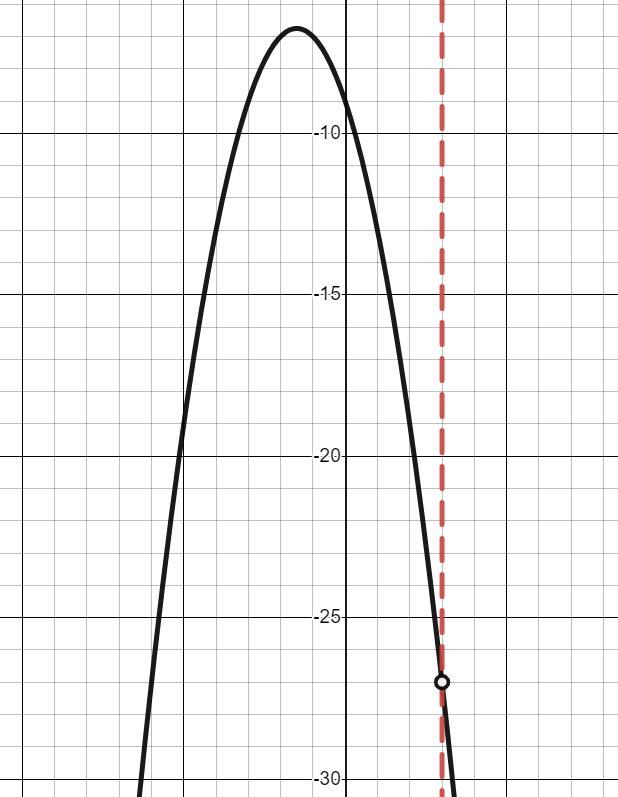
Построим полученное в координатах (x; a).

Итого:

1) При уравнение не имеет корней.

2) При уравнение имеет ровно один корень.

3) При уравнение имеет ровно два корня.

Задание выполнено!