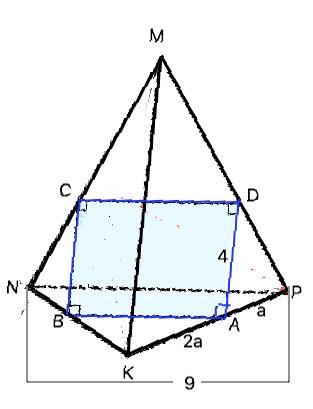
При проведении через точку А, взятую на ребре PK тетраэдра MNPK,параллельной плоскости к ребрам PN и KM, в данном сечение образовался прямоугольник ABCD. Найти периметр ABCD, если AB параллельна PN, PA:AK=1:2, PN=9 дм, AD=4 дм
Ответы на вопрос
Ответил Hrisula
0
Ответ: 20 см
Объяснение: Рассмотрим основание NPK данного тетраэдра. Сторона АВ получившегося прямоугольника параллельна стороне PN треугольника NPK. Треугольники КВА и КNP подобны по двум углам: угол К общий, углы КАВ и КРN равны как соответственные при пересечении параллельных АВ и PN секущей КР.
Из данного в условии отношения отрезков ребра РК примем РА=а, АК=2а, ⇒ РК=РА+АК=а+2а=3а. Коэффициент подобия РК:АК=3:2 . ⇒ PN:АВ=3:2, откуда АВ=2/3 PN=9•2/3=6 дм.
Противоположные стороны прямоугольника равны. Р(АВСD)=2•(АВ+АD)=2•(6+4)=20 (см)
Приложения:
Новые вопросы