при каких значениях параметра b уравнение 1/3x^3-x=b имеет 3 корня

При каких значениях параметра b уравнение 1/3x^3-x=b имеет 3 корня

решим графически

зададим функцию 

y=¹/₃ x³-x и у=в

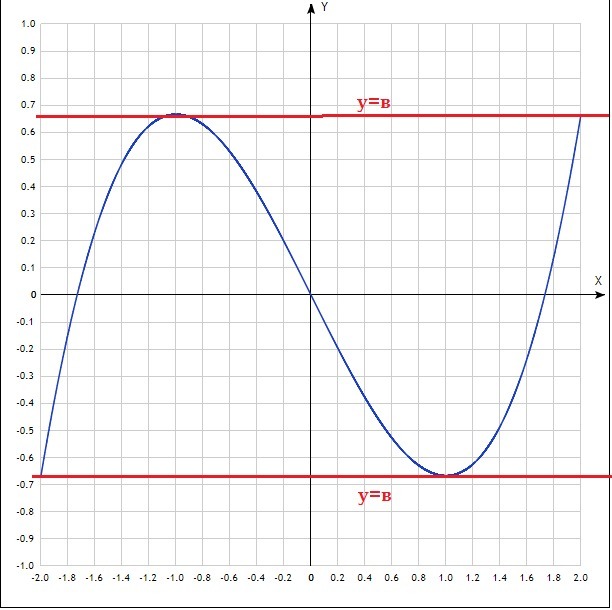
построим график (смотри приложение)

видим что три корня будут в промежутках между точками максимума и минимума функции

найдем эти точки

для этого найдем производную 

y`=(¹/₃ x³-x)`=³/₃ x²-1=x²-1

y`=0; x²-1=0; x²=1; x=1 или х=-1

точка х=1 точка максимума, точка х=-1 точка минимума

y(-1)=¹/₃*(-1)-(-1)=-¹/₃+1=²/₃
y(1)=¹/₃*1-1=¹/₃-1= -²/₃

тогда у=в - прямая которая лежит в промежутке (-²/₃; ²/₃)