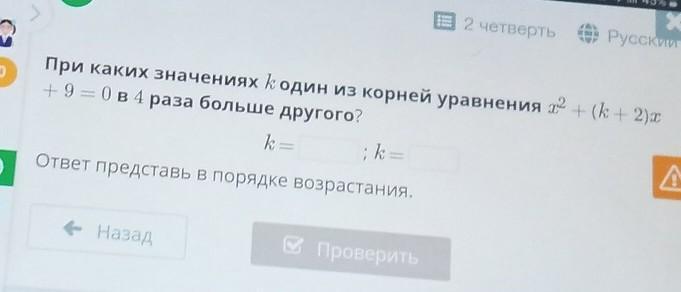
Алгебра, вопрос задал 777wktzt , 2 года назад

При каких значениях K один из корней уравнения х ² + (к+2)х+9=0 в 4 раза больше другого пожалуйста умоляю ответьте кто-нибудь пожалуйста помогите мне ​

Приложения:

Ответы на вопрос

Ответил axatar
0

Ответ:

k = -9,5,   k=5,5

Объяснение:

Пусть x₁ и x₂ корни уравнения. Применим теорему Виета:

\displaystyle \tt \left \{ {{x_1+x_2=-(k+2)} \atop {x_1 \cdot x_2=9}} \right. .

По условию задачи x₂ = 4·x₁. Если подставим в систему, то получим:

\displaystyle \tt \left \{ {{x_1+4 \cdot x_1=-(k+2)} \atop {x_1 \cdot 4 \cdot x_1=9}} \right. \Leftrightarrow \left \{ {{5 \cdot x_1=-(k+2)} \atop { 4 \cdot x_1^2=9}} \right. \Leftrightarrow \left \{ {{k+2=-5 \cdot x_1} \atop { x_1^2=\dfrac{9}{4} }} \right. \Leftrightarrow \\\\\Leftrightarrow \left \{ {{k=-5 \cdot x_1-2} \atop { x_1=\pm \sqrt{\dfrac{9}{4} } }} \right. \Leftrightarrow \left \{ {{k=-5 \cdot x_1-2} \atop { x_1=\pm \dfrac{3}{2} }} \right. .

Для каждого значения x₁ находим k:

\displaystyle \tt x_1= \dfrac{3}{2} , \;\; k=-5 \cdot \dfrac{3}{2}-2=-\dfrac{15}{2}- \dfrac{4}{2}= -\dfrac{19}{2}=-9,5;\\\\x_2= -\dfrac{3}{2} , \;\; k=-5 \cdot (- \dfrac{3}{2})-2=\dfrac{15}{2}- \dfrac{4}{2}= \dfrac{11}{2}=5,5.

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Русский язык, 1 год назад
обозначить орфограмму слов: ПРЕБЫВАТЬ на вокзале,РАСПОЛОЖИТЬСЯ на перроне, ПРИКОСНУТЬСЯ к фуражке Заранее огромное спасибо! Вот пример как сделать: Прибывать (присоед.) и т.д. Срочно!
Русский язык, 1 год назад
Сочинение про размышление звёзд 8 предложение...
Биология, 2 года назад
помогите сделать 3 и 4 задачу пожалйста...
Алгебра, 2 года назад
6 * 10<-2 и 6 * 10<-1 < - степень ​...
Математика, 7 лет назад
Помогите пожалуйста срочно нужно...
Литература, 7 лет назад
вчем проявляется проявлина сила герасима из сказки муму...