Алгебра, вопрос задал Женя321 , 9 лет назад

Представьте в виде многочлена выражение

Приложения:

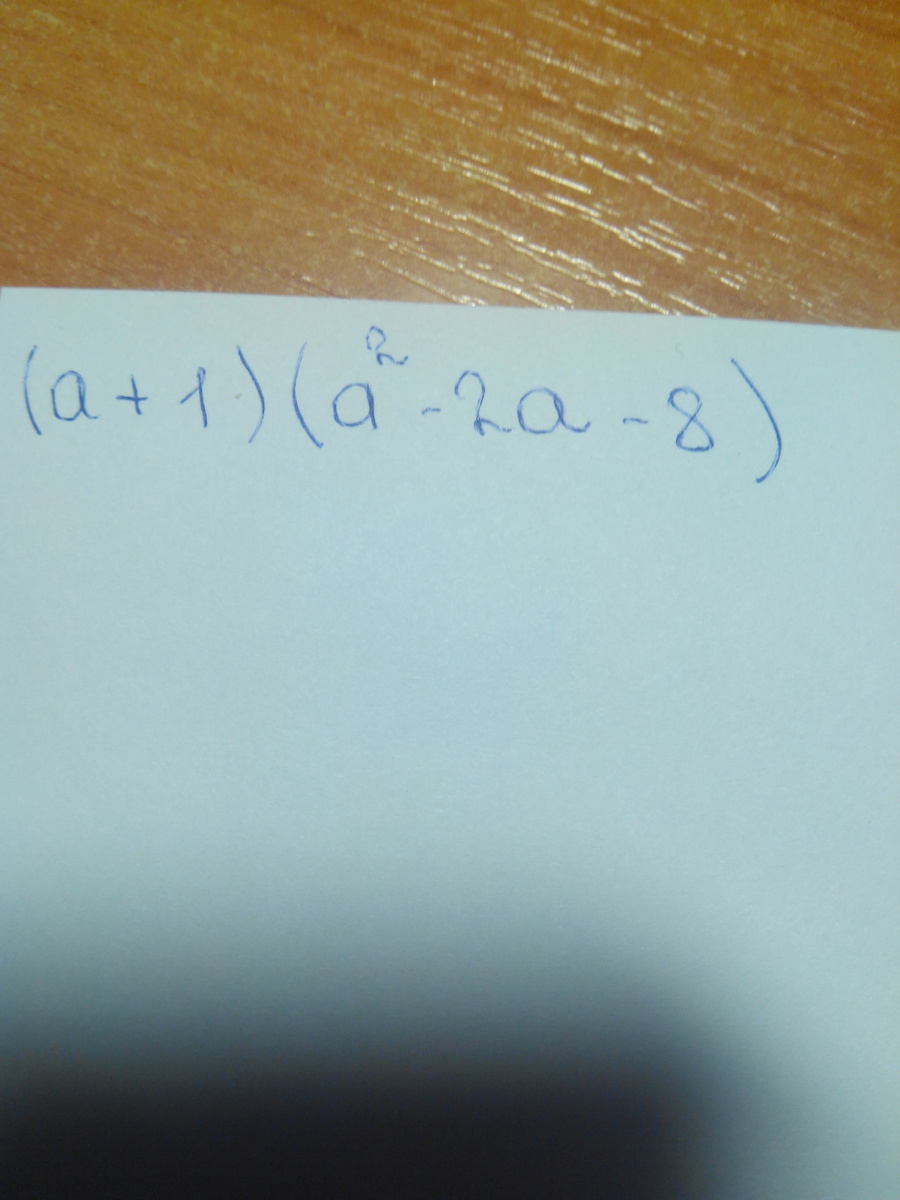
Ответы на вопрос

Ответил bestiacat

Сначала решим квадратное уравнение
коэффициенты квадратного уравнения а=1, b=-2, c=-8
Найдем дискриминант: D=b2-4ac=(-2)2-4*1*(-8)=4+32=36
Найдем корни уравнения
$x_{1} = frac{-b+ sqrt{D} }{2a}= frac{2+ sqrt{36} }{2*1} frac{2+6}{2}=4$
$x_{2} = frac{-b- sqrt{D} }{2a}= frac{2- sqrt{36} }{2*1} frac{2-6}{2}=-2$
Разложим квадратный трехчлен по формуле $a x^{2} +bx-c=a(x- x_{1} )(x- x_{2} )$
соответственно $a^{2} -2a-8=(a-4)(a+2)$
исходное выражение можно представить в следующем виде
$(a+1)( a^{2} -2a-8)=(a+1)(a-4)(a+2)$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська мова, 2 года назад

Виконай вправу «Кола воді». До кожно букви слова «сфера» добери слово. Склади речення, які утворять зв'язний текст.

Литература, 2 года назад

Как понял свою задачу редактора герой памфлета? Удалось ли, по его мнению, её достигнуть? Можете ли вы сказать,что некоторые современные печатные издания пользуются теми же приёмами? Марк Твен "как...

Алгебра, 9 лет назад

СРОЧНО !!!! Найдите сумму первых 10 членов арифметической прогресссии; b1=-17; d=6...

Алгебра, 9 лет назад

Как с помощью четырех колышков,двух колечек и веревок привязать козу так,чтобы она ела траву только в точках данного прямоугольника?

Алгебра, 9 лет назад

сократите дробь (8y^2-2)/(8-16y) ...

История, 9 лет назад

Итоги Февральской революции 1848 г ?