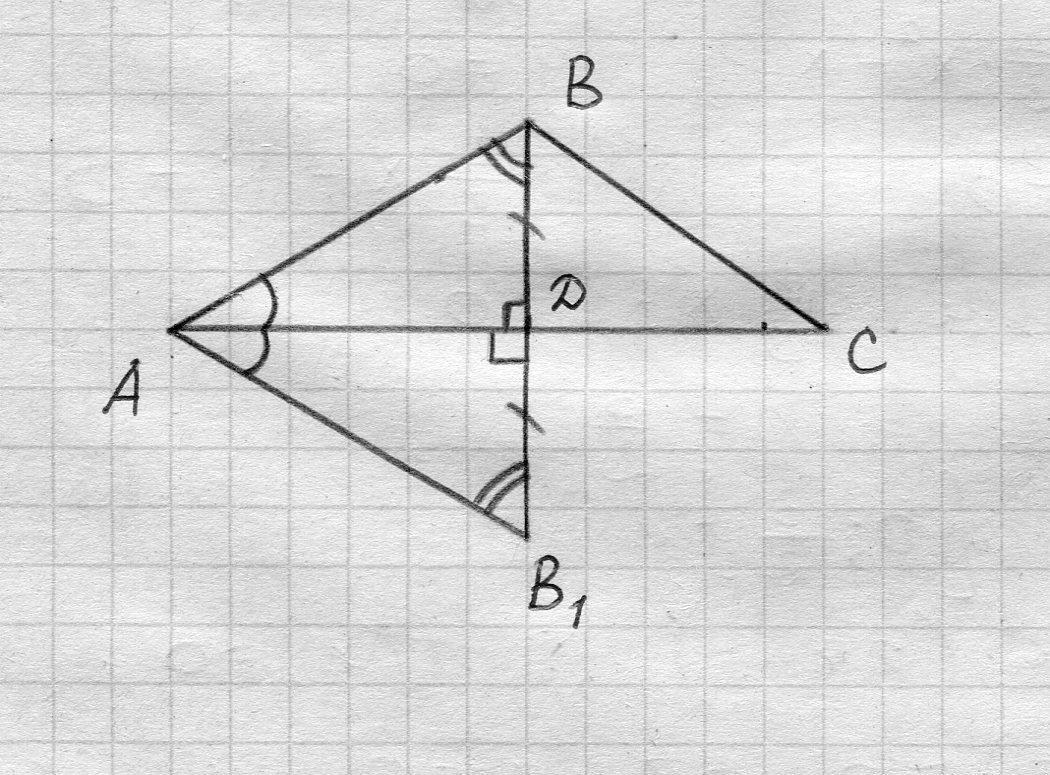
Пожалуйста решите задачу ( без ctg) Задача 733

Ответы на вопрос
Сначала найдем высоту BD, из прямоугольного ΔBCD по теореме Пифагора
BD² = BC² - CD² = 37 - 5² = 37 - 25 = 12,
BD = √(12) = 2*√3 см.
Из прямоугольного ΔABD найдем:
∠ABD = 180° - 90° - ∠BAD = 90° - 30° = 60°.
Продолжим отрезок BD за точку D и отложим на прямой BD отрезок
DB₁ = BD. И проведём отрезок AB₁. Тогда прямоугольный
ΔABD = ΔAB₁D (по двум катетам и прямому углу).
Тогда ∠AB₁D = ∠ABD = 60° и тогда 30° = ∠A = ∠BAD = ∠B₁AD, и
∠BAB₁ = ∠BAD + ∠B₁AD = 30° + 30° = 60°
Получаем, что в ΔBAB₁ все углы по 60°. Против равных углов в треугольнике лежат равные стороны, поэтому ΔBAB₁ равносторонний, поэтому AB = BB₁,
BB₁ = BD+DB₁ = 2*BD = 2*2*√3 = 4*√3 и
AB = BB₁ = 4*√3.
Из прямоугольного ΔABD по теореме Пифагора найдем AD:
AD² = AB² - BD² = (4*√3)² - (2*√3)² = 16*3 - 4*3 = 12*3 = 36,
AD = √36 = 6 см.
AC = AD+CD = 6см+5см = 11см.
S(ΔABC) = (1/2)*AC*BD = (1/2)*(11см)*(2*√3 см) = 11*√3 см²