Математика, вопрос задал ganeevaalfiya19 , 6 лет назад

Пожалуйста решите пример с решением

Приложения:

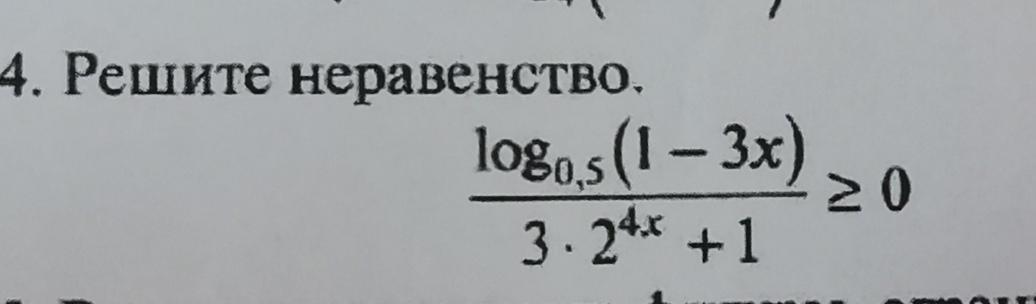
Ответы на вопрос

Ответил vika20035cher

Ответ:

x∈[0, $\frac{1}{3}$ )

Пошаговое объяснение:

x∈(-∞, $\frac{1}{3}$ ) - это область допустимых значений

$\frac{logx_{0,5(1-3x)} }{3*2^{4x} +1} \geq 0$ , x∈(-∞, $\frac{1}{3}$ )

$-\frac{log_{2(1-3x)} }{3*16^{x} +1} \geq 0$

Меняем знак так как стоит минус перед выражением!

$\frac{log_{2(1-3x)} }{3*16^{x} +1}\leq 0$

Поскольку знаменатель всегда положителен, мы просто определяем числитель:

$log_{2} (1-3x)\leq 0\\\\1-3x\leq 2^{0} \\\\1-3x\leq 1\\\\\--3x\leq 0\\\\x\geq 0$

x∈[0, $\frac{1}{3}$ )

-∞ ------------------ $\frac{1}{3}$ ------------------>

--------------0---------------------->+∞

и типо получается что от 0 до одной трети

Новые вопросы

Қазақ тiлi, 1 год назад

Русский язык, 1 год назад

Русский язык, 6 лет назад

Қазақ тiлi, 6 лет назад

Математика, 8 лет назад

Биология, 8 лет назад